Full solution
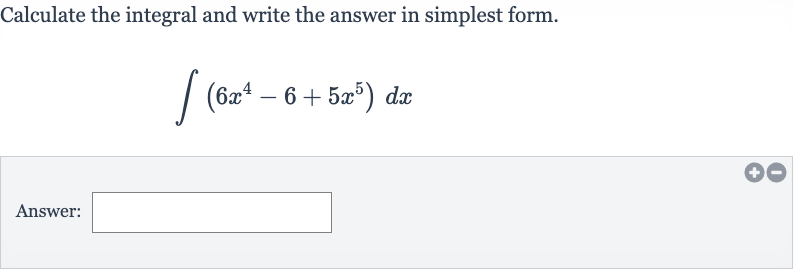
Q. Calculate the integral and write the answer in simplest form.Answer:
- Given integral function: We are given the integral of a polynomial function: To solve this, we will integrate each term separately using the power rule for integration, which states that for any real number .
- Integrating : First, we integrate the term :
- Integrating : Next, we integrate the constant term :
- Integrating : Finally, we integrate the term :
- Combining integrations: Now, we combine the results of the integrations and add the constant of integration :
- Simplifying expression: We simplify the expression by multiplying the coefficients:
- Final answer: The final answer in simplest form is: