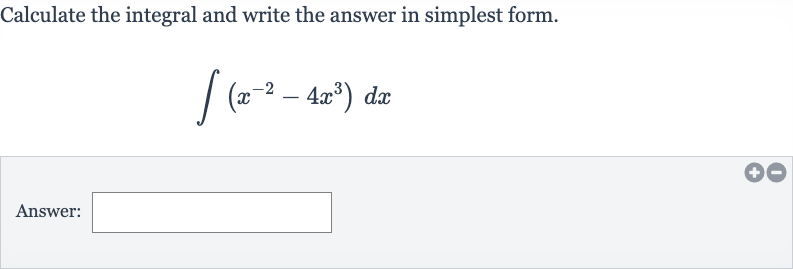
Calculate the integral and write the answer in simplest form. int(x^(-2)-4x^(3))dx Answer:

Question

Calculate the integral and write the answer in simplest form.  int(x^(-2)-4x^(3))dx Answer:

Bytelearn · Accepted Answer

Integrate each term separately: We are given the integral of the function x^(-2) - 4x^(3). We will integrate each term separately. The integral of x^(-2) is -x^(-1) or -1/x, and the integral of -4x^(3) is -4x^(4)/4 or -x^(4). So, the integral of the given function is: ∫(x^(-2) - 4x^(3))dx = ∫x^(-2)dx - ∫4x^(3)dxIntegrate x^(-2): Now we will integrate each term separately. For the first term: ∫x^(-2)dx = ∫x^(-2 + 1)/( -2 + 1)dx = -x^(-1) + C1 For the second term: ∫4x^(3)dx = 4∫x^(3)dx = 4(x^(3 + 1)/(3 + 1)) = x^(4) + C2Integrate -4x^(3): Combining the two integrals, we get: ∫(x^(-2) - 4x^(3))dx = -x^(-1) - x^(4) + C Where C is the constant of integration, which is a combination of C1 and C2.Combine the integrals: We can simplify the expression by combining the constants of integration into a single constant, which we will also call C. So the final answer is: ∫(x^(-2) - 4x^(3))dx = -1/x - x^(4) + C

Calculate the integral and write the answer in simplest form. $\newline$ $\int\left(x^{-2}-4 x^{3}\right) d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Calculate the integral and write the answer in simplest form.\newline∫(x−2−4x3)dx \int\left(x^{-2}-4 x^{3}\right) d x ∫(x−2−4x3)dx\newlineAnswer:

Calculate the integral and write the answer in simplest form. $\newline$ $\int\left(x^{-2}-4 x^{3}\right) d x$ $\newline$ Answer: