Full solution
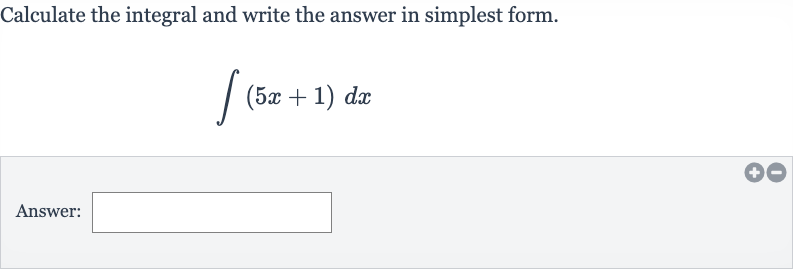
Q. Calculate the integral and write the answer in simplest form.Answer:
- Recognize Integral as Sum: Recognize the integral as the sum of two simpler integrals. The integral of a sum is the sum of the integrals, so we can write: \int(\(5x+)\,dx = \int x\,dx + \int \,dx
- Integrate Each Term: Integrate each term separately.The integral of with respect to is , because the antiderivative of is for .The integral of with respect to is , because the antiderivative of a constant is the constant times the variable.So we have:
- Combine Results and Add Constant: Combine the results of the two integrals and add the constant of integration. The combined result is: where is the constant of integration.