Full solution
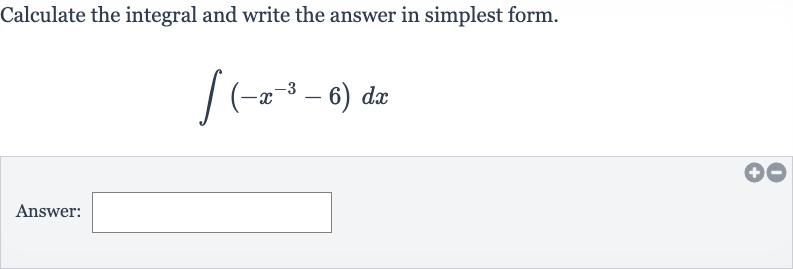
Q. Calculate the integral and write the answer in simplest form.Answer:
- Write Integral: Write down the integral to be solved.
- Split Integral: Split the integral into two separate integrals.
- Integrate First Term: Integrate the first term .
- Integrate Second Term: Integrate the second term .
- Combine Results: Combine the results of the two integrals and add the constant of integration .
- Final Answer: Write the final answer in simplest form.The indefinite integral of the function with respect to is .