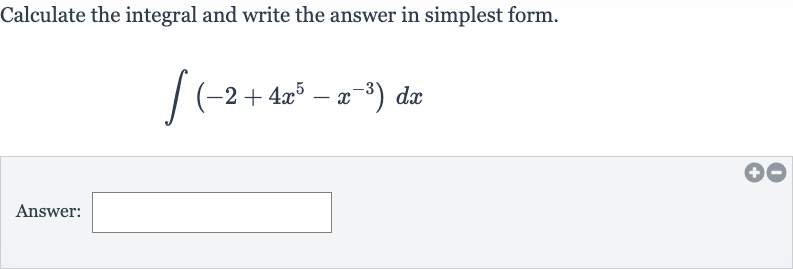
Calculate the integral and write the answer in simplest form. int(-2+4x^(5)-x^(-3))dx Answer:

Question

Calculate the integral and write the answer in simplest form.  int(-2+4x^(5)-x^(-3))dx Answer:

Bytelearn · Accepted Answer

Break down the integral: Break down the integral into separate terms. ∫(-2 + 4x^5 - x^(-3))dx = ∫(-2)dx + ∫(4x^5)dx - ∫(x^(-3))dxIntegrate each term separately: Integrate each term separately. For the first term, ∫(-2)dx, the integral of a constant -2 with respect to x is -2x. For the second term, ∫(4x^5)dx, we use the power rule for integration, which states that ∫(x^n)dx = x^(n+1)/(n+1) for n ≠ -1. Therefore, the integral of 4x^5 with respect to x is (4/6)x^(5+1) or (2/3)x^6. For the third term, -∫(x^(-3))dx, we again use the power rule for integration. The integral of x^(-3) with respect to x is x^(-3+1)/(-3+1) or -x^(-2)/2.Combine and simplify: Combine the results of the integrals and simplify. The combined integral is -2x + (2/3)x^6 - (-1/2)x^(-2). Simplify the expression by combining like terms and adjusting signs. The simplified result is -2x + (2/3)x^6 + (1/2)x^(-2).Add constant of integration: Add the constant of integration C to the result. The final answer with the constant of integration is -2x + (2/3)x^6 + (1/2)x^(-2) + C.

Calculate the integral and write the answer in simplest form. $\newline$ $\int\left(-2+4 x^{5}-x^{-3}\right) d x$ $\newline$ Answer:

Full solution

More problems from Find indefinite integrals using the substitution

Related topics

Calculate the integral and write the answer in simplest form.\newline∫(−2+4x5−x−3)dx \int\left(-2+4 x^{5}-x^{-3}\right) d x ∫(−2+4x5−x−3)dx\newlineAnswer:

Calculate the integral and write the answer in simplest form. $\newline$ $\int\left(-2+4 x^{5}-x^{-3}\right) d x$ $\newline$ Answer: