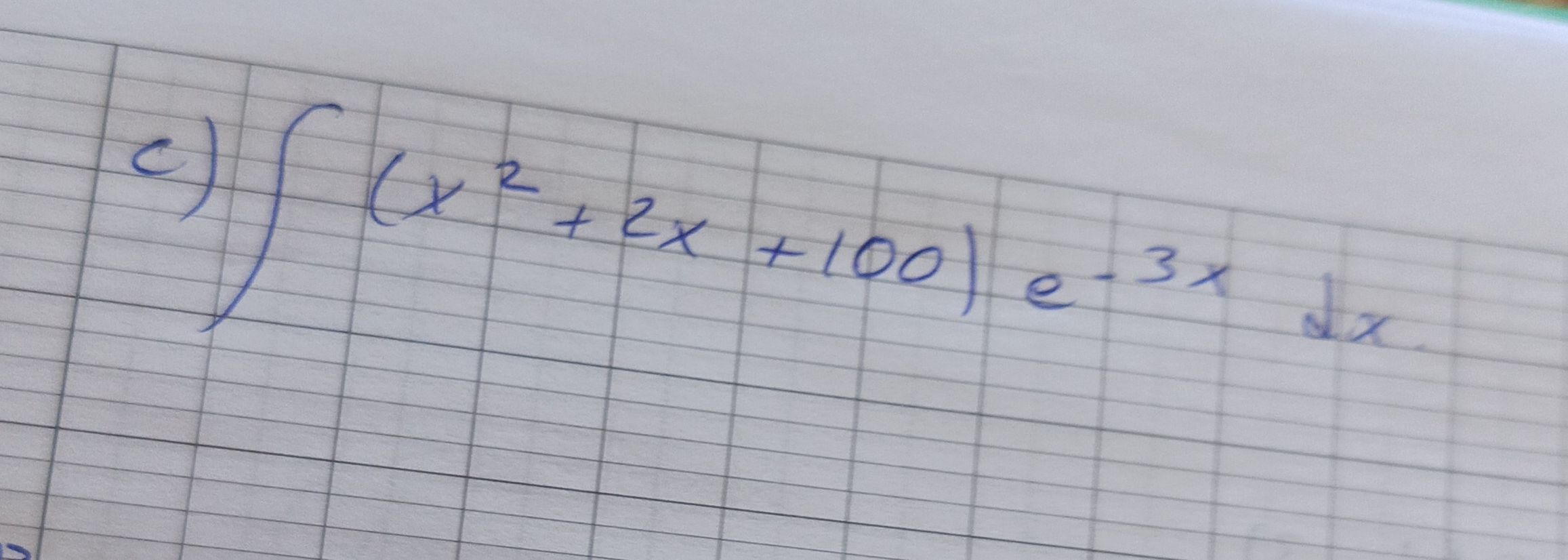Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

int(x^(2)+2x+100)e^(-3x)dx=

∫(x2+2x+100)e−3xdx \int\left(x^{2}+2 x+100\right) e^{-3 x} d x =

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Gaussian integralright chevron icon

Full solution

Q. ∫(x2+2x+100)e−3xdx \int\left(x^{2}+2 x+100\right) e^{-3 x} d x =
  1. Identify integral: Identify the integral to be solved.\newlineWe need to find the integral of the function (x2+2x+100)e−3x(x^2 + 2x + 100)e^{-3x} with respect to xx.
  2. Apply integration by parts: Apply integration by parts.\newlineIntegration by parts formula is ∫u dv=uv−∫v du\int u \, dv = uv - \int v \, du.\newlineLet u=x2+2x+100u = x^2 + 2x + 100, which means du=(2x+2)dxdu = (2x + 2)dx.\newlineLet dv=e−3xdxdv = e^{-3x}dx, which means v=−13e−3xv = -\frac{1}{3} e^{-3x}.
  3. Perform first integration: Perform the first integration by parts.\newlineUsing the formula, we get:\newline∫(x2+2x+100)e−3x dx=(x2+2x+100)(−13e−3x)−∫(−13e−3x)(2x+2) dx\int(x^2 + 2x + 100)e^{-3x}\,dx = (x^2 + 2x + 100)(-\frac{1}{3} e^{-3x}) - \int(-\frac{1}{3} e^{-3x})(2x + 2)\,dx
  4. Simplify expression: Simplify the expression.\newline=−(13)(x2+2x+100)e−3x+(23)∫(x+1)e−3xdx= -(\frac{1}{3})(x^2 + 2x + 100)e^{-3x} + (\frac{2}{3})\int(x + 1)e^{-3x}dx\newlineNow we need to integrate (x+1)e−3x(x + 1)e^{-3x} with respect to xx.
  5. Apply integration by parts again: Apply integration by parts again for the remaining integral.\newlineLet u=x+1u = x + 1, which means du=dxdu = dx.\newlineLet dv=e−3xdxdv = e^{-3x}dx, which means v=−13e−3xv = -\frac{1}{3} e^{-3x}.
  6. Perform second integration: Perform the second integration by parts.\newline∫(x+1)e−3xdx=(x+1)(−13e−3x)−∫(−13e−3x)(1)dx\int(x + 1)e^{-3x}dx = (x + 1)(-\frac{1}{3} e^{-3x}) - \int(-\frac{1}{3} e^{-3x})(1)dx
  7. Integrate e−3xe^{-3x}: Simplify the expression.\newline=−13(x+1)e−3x+13∫e−3x dx= -\frac{1}{3}(x + 1)e^{-3x} + \frac{1}{3}\int e^{-3x}\,dx\newlineNow we need to integrate e−3xe^{-3x} with respect to xx.
  8. Combine all parts: Integrate e−3xe^{-3x} with respect to xx.
    ∫e−3x dx=−13e−3x+C\int e^{-3x}\,dx = -\frac{1}{3} e^{-3x} + C, where CC is the constant of integration.
  9. Simplify final expression: Combine all parts together.\newlinePutting it all together, we have:\newline∫(x2+2x+100)e(−3x)dx=−(13)(x2+2x+100)e(−3x)+(23)(−(13)(x+1)e(−3x)+(13)∫e(−3x)dx)\int(x^2 + 2x + 100)e^{(-3x)}dx = -(\frac{1}{3})(x^2 + 2x + 100)e^{(-3x)} + (\frac{2}{3})(-(\frac{1}{3})(x + 1)e^{(-3x)} + (\frac{1}{3})\int e^{(-3x)}dx)\newline=−(13)(x2+2x+100)e(−3x)−(29)(x+1)e(−3x)−(29)(−13e(−3x))+C= -(\frac{1}{3})(x^2 + 2x + 100)e^{(-3x)} - (\frac{2}{9})(x + 1)e^{(-3x)} - (\frac{2}{9})(-\frac{1}{3} e^{(-3x)}) + C
  10. Simplify final expression: Combine all parts together.\newlinePutting it all together, we have:\newline∫(x2+2x+100)e−3x dx=−(13)(x2+2x+100)e−3x+(23)(−(13)(x+1)e−3x+(13)∫e−3x dx)\int(x^2 + 2x + 100)e^{-3x}\,dx = -(\frac{1}{3})(x^2 + 2x + 100)e^{-3x} + (\frac{2}{3})(-(\frac{1}{3})(x + 1)e^{-3x} + (\frac{1}{3})\int e^{-3x}\,dx)\newline=−(13)(x2+2x+100)e−3x−(29)(x+1)e−3x−(29)(−13e−3x)+C= -(\frac{1}{3})(x^2 + 2x + 100)e^{-3x} - (\frac{2}{9})(x + 1)e^{-3x} - (\frac{2}{9})(-\frac{1}{3} e^{-3x}) + C Simplify the final expression.\newline=−(13)(x2+2x+100)e−3x−(29)(x+1)e−3x+(227)e−3x+C= -(\frac{1}{3})(x^2 + 2x + 100)e^{-3x} - (\frac{2}{9})(x + 1)e^{-3x} + (\frac{2}{27})e^{-3x} + C\newline=−e−3x(13x2+23x+1003+29x+29−227)+C= -e^{-3x}(\frac{1}{3} x^2 + \frac{2}{3} x + \frac{100}{3} + \frac{2}{9} x + \frac{2}{9} - \frac{2}{27}) + C\newline=−e−3x(13x2+89x+29827)+C= -e^{-3x}(\frac{1}{3} x^2 + \frac{8}{9} x + \frac{298}{27}) + C

More problems from Gaussian integral

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 3 months ago

View all (20)