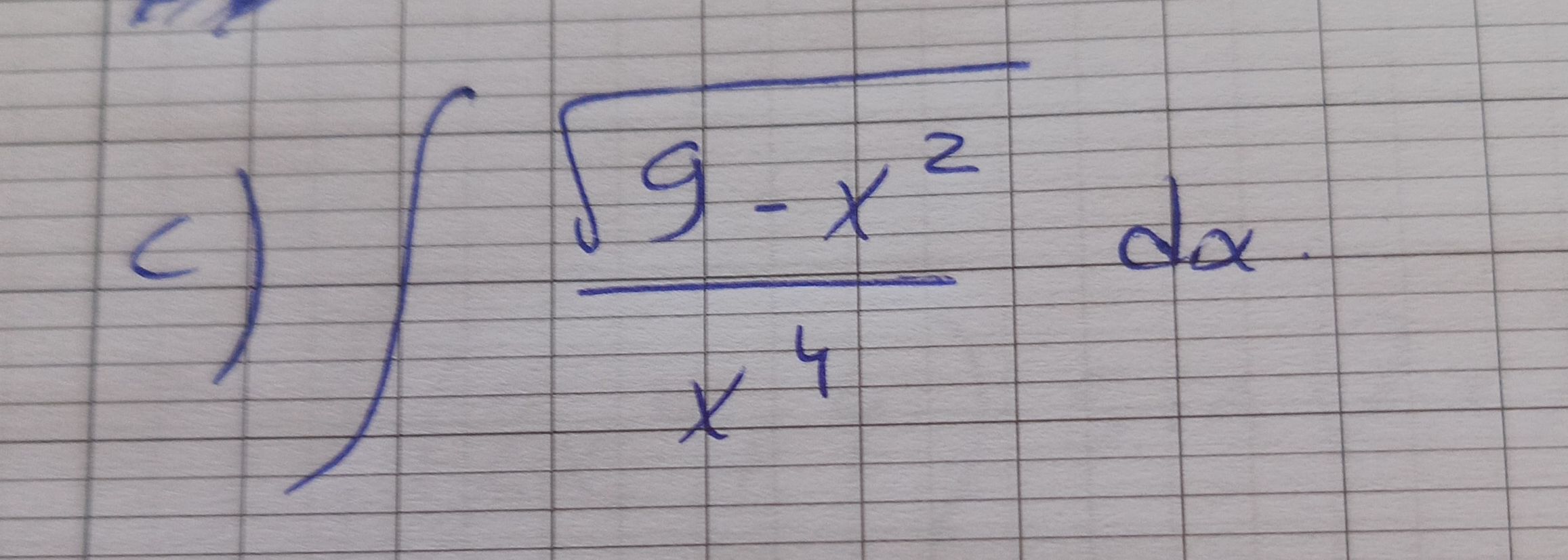Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

int(sqrt(9-x^(2)))/(x^(4))dx

∫9−x2x4dx \int \frac{\sqrt{9-x^{2}}}{x^{4}} d x =

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find indefinite integrals using the substitutionright chevron icon

Full solution

Q. ∫9−x2x4dx \int \frac{\sqrt{9-x^{2}}}{x^{4}} d x =
  1. Recognize Standard Form: Recognize the integral as a standard form that can be solved using trigonometric substitution. The integral is ∫9−x2x4dx\int\frac{\sqrt{9-x^{2}}}{x^{4}}dx. We can use the substitution x=3sin⁡(θ)x = 3\sin(\theta), where −π2≤θ≤π2-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}, because 9−x2\sqrt{9-x^{2}} suggests a trigonometric identity sin⁡2(θ)+cos⁡2(θ)=1\sin^{2}(\theta) + \cos^{2}(\theta) = 1.
  2. Find dxdx in terms: Differentiate x=3sin⁡(θ)x = 3\sin(\theta) to find dxdx in terms of d(θ)d(\theta).\newlinedxd(θ)=3cos⁡(θ)\frac{dx}{d(\theta)} = 3\cos(\theta)\newlinedx=3cos⁡(θ)d(θ)dx = 3\cos(\theta)d(\theta)
  3. Substitute xx and dxdx: Substitute xx and dxdx in the integral with the expressions involving theta.∫9−x2x4dx=∫9−(3sin⁡(θ))2(3sin⁡(θ))4⋅3cos⁡(θ)d(θ)\int\frac{\sqrt{9-x^{2}}}{x^{4}}dx = \int\frac{\sqrt{9-(3\sin(\theta))^{2}}}{(3\sin(\theta))^{4}} \cdot 3\cos(\theta)d(\theta)Simplify the expression inside the integral.=∫9−9sin⁡2(θ)27sin⁡4(θ)⋅3cos⁡(θ)d(θ)= \int\frac{\sqrt{9-9\sin^{2}(\theta)}}{27\sin^{4}(\theta)} \cdot 3\cos(\theta)d(\theta)=∫9(1−sin⁡2(θ))27sin⁡4(θ)⋅3cos⁡(θ)d(θ)= \int\frac{\sqrt{9(1-\sin^{2}(\theta))}}{27\sin^{4}(\theta)} \cdot 3\cos(\theta)d(\theta)=∫9cos⁡2(θ)27sin⁡4(θ)⋅3cos⁡(θ)d(θ)= \int\frac{\sqrt{9\cos^{2}(\theta)}}{27\sin^{4}(\theta)} \cdot 3\cos(\theta)d(\theta)=∫3cos⁡(θ)27sin⁡4(θ)⋅3cos⁡(θ)d(θ)= \int\frac{3\cos(\theta)}{27\sin^{4}(\theta)} \cdot 3\cos(\theta)d(\theta)=∫9cos⁡2(θ)27sin⁡4(θ)d(θ)= \int\frac{9\cos^{2}(\theta)}{27\sin^{4}(\theta)}d(\theta)=∫cos⁡2(θ)3sin⁡4(θ)d(θ)= \int\frac{\cos^{2}(\theta)}{3\sin^{4}(\theta)}d(\theta)
  4. Simplify Expression: Simplify the integral further by using the trigonometric identity cos⁡2(θ)=1−sin⁡2(θ)\cos^2(\theta) = 1 - \sin^2(\theta).
    ∫(cos⁡2(θ))/(3sin⁡4(θ))d(θ)=∫((1−sin⁡2(θ)))/(3sin⁡4(θ))d(θ)\int(\cos^2(\theta))/(3\sin^4(\theta))d(\theta) = \int((1 - \sin^2(\theta)))/(3\sin^4(\theta))d(\theta)
    Split the integral into two parts.
    = 13∫(1sin⁡4(θ))d(θ)−13∫(sin⁡2(θ)sin⁡4(θ))d(θ)\frac{1}{3} \int(\frac{1}{\sin^4(\theta)})d(\theta) - \frac{1}{3} \int(\frac{\sin^2(\theta)}{\sin^4(\theta)})d(\theta)
    = 13∫(csc⁡4(θ))d(θ)−13∫(1sin⁡2(θ))d(θ)\frac{1}{3} \int(\csc^4(\theta))d(\theta) - \frac{1}{3} \int(\frac{1}{\sin^2(\theta)})d(\theta)
    = 13∫(csc⁡4(θ))d(θ)−13∫(csc⁡2(θ))d(θ)\frac{1}{3} \int(\csc^4(\theta))d(\theta) - \frac{1}{3} \int(\csc^2(\theta))d(\theta)
  5. Use Trig Identity: Integrate each part separately.\newlineThe integral of csc⁡4(θ)\csc^4(\theta) is not elementary, and the integral of csc⁡2(θ)\csc^2(\theta) is −cot⁡(θ)-\cot(\theta).\newlineHowever, we can use integration by parts for the first integral or look for a reduction formula. Since the integral of csc⁡4(θ)\csc^4(\theta) is not straightforward, we will use integration by parts.\newlineLet u=csc⁡2(θ)u = \csc^2(\theta), dv=csc⁡2(θ)d(θ)dv = \csc^2(\theta)d(\theta), then du=−2csc⁡2(θ)cot⁡(θ)d(θ)du = -2\csc^2(\theta)\cot(\theta)d(\theta), v=−cot⁡(θ)v = -\cot(\theta).
  6. Apply Integration by Parts: Apply integration by parts to the first integral. \newline∫csc⁡4(θ) d(θ)=u⋅v−∫(v⋅du)\int \csc^4(\theta)\,d(\theta) = u \cdot v - \int(v \cdot du)\newline=−csc⁡2(θ)cot⁡(θ)−∫(−cot⁡(θ)⋅(−2csc⁡2(θ)cot⁡(θ)) d(θ))= -\csc^2(\theta)\cot(\theta) - \int(-\cot(\theta) \cdot (-2\csc^2(\theta)\cot(\theta))\,d(\theta))\newline=−csc⁡2(θ)cot⁡(θ)+2∫(csc⁡2(θ)cot⁡2(θ) d(θ))= -\csc^2(\theta)\cot(\theta) + 2\int(\csc^2(\theta)\cot^2(\theta)\,d(\theta))
  7. Correct Integration Mistake: Realize that there is a mistake in the previous step.\newlineThe integration by parts was not applied correctly. The correct application should be:\newline∫csc⁡4(θ) d(θ)=u⋅v−∫(v⋅du)\int \csc^4(\theta) \, d(\theta) = u \cdot v - \int(v \cdot du)\newline= −csc⁡2(θ)cot⁡(θ)+2∫(cot⁡2(θ)csc⁡2(θ) d(θ))-\csc^2(\theta)\cot(\theta) + 2\int(\cot^2(\theta)\csc^2(\theta)\,d(\theta))\newlineHowever, this integral is still not elementary and requires further reduction, which is not straightforward. We need to reconsider our approach to this problem.

More problems from Find indefinite integrals using the substitution

Question
Evaluate the integral.\newline∫−x4−3xdx \int-x 4^{-3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x3e−2xdx \int 6 x^{3} e^{-2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫x53xdx \int x 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xe2xdx \int-2 x e^{2 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−2xcos⁡(−2x)dx \int-2 x \cos (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−xcos⁡(−3x)dx \int-x \cos (-3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x253xdx \int 6 x^{2} 5^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−6x4−4xdx \int-6 x 4^{-4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫6x223xdx \int 6 x^{2} 2^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−3xsin⁡(−2x)dx \int-3 x \sin (-2 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

View all (263)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant