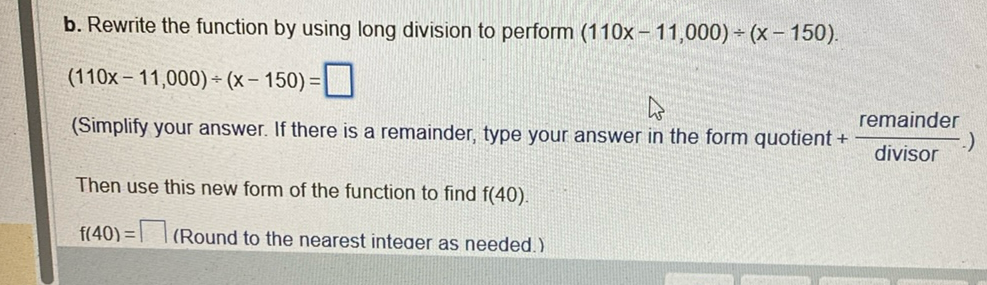
Rewrite the function by using long division to perform (110 x-11,000)÷(x-150). (110 x-11,000)÷(x-150)=◻ (Simplify your answer. If there is a remainder, type your answer in the form quotient +(remainder)/(divisor) .) Then use this new form of the function to find f(40). f(40)=◻ (Round to the nearest inteder as needed.)

Question

Bytelearn · Accepted Answer

Divide 110x by x: Divide 110x by x to get 110. Write 110 above the division bar.Multiply and Subtract: Multiply (x - 150) by 110 to get 110x - 16,500. Subtract this from 110x - 11,000.Calculate Remainder: After subtraction, we get 11,000 - 16,500 which is -5,500. This is our remainder.Write Final Function: So, the result of the division is 110 with a remainder of -5,500. Write the function as 110 + (-5500)/(x - 150).Substitute x in Function: Now, to find f(40), substitute x with 40 in the new form of the function: f(40) = 110 + (-5500)/(40 - 150).Calculate Denominator: Calculate the denominator of the fraction: 40 - 150 = -110.Calculate Fraction: Now, calculate the fraction: (-5500)/(-110) = 50.Add to Get f(40): Add this to 110 to get f(40): f(40) = 110 + 50.Final Result: So, f(40) equals 160. Round to the nearest integer, which is still 160.

Full solution

More problems from Find indefinite integrals using the substitution

Related topics