Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

20:16 A X
9=
(1) 以ล
Jo Skyscanner
Guwahati to Shillong
from Rs696
View
PREVIOUS
NEXT
MHT CET 2021 22th September Evening Shift
1
MCQ (Single Correct Answer)

+2

-0
(4)
The particular solution of the differential equation
(dy)/(dx)=(y+1)/(x^(2)-x), when
x=2 and
y=1 is
A)
xy=4x-6
B
xy=2x-2
Correct Answer
c)
xy=x-2
D
xy=-x+4

The particular solution of the differential equation $\newline$ $\frac{dy}{dx}=\frac{y+1}{x^{2}-x}$ , when $\newline$ $x=2$ and $\newline$ $y=1$ is $\newline$ A) $xy=4x-6$ $\newline$ B) $xy=2x-2$ $\newline$ C) $xy=x-2$ $\newline$ D) $xy=-x+4$

View step-by-step help

View step-by-step help

Full solution

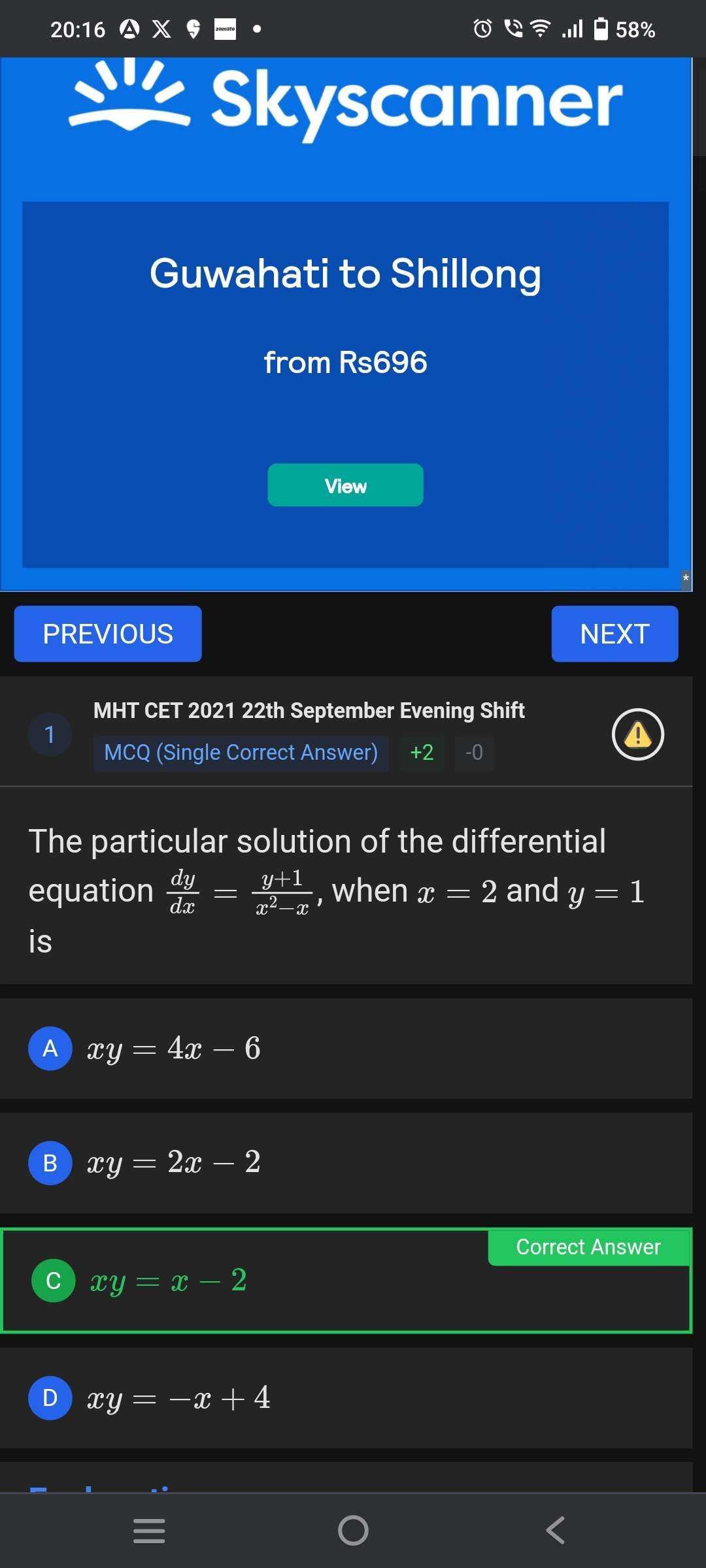
Q. The particular solution of the differential equation

\newline

\frac{dy}{dx}=\frac{y+1}{x^{2}-x}

, when

\newline

x=2

and

\newline

y=1

is

\newline

A)

xy=4x-6

\newline

B)

xy=2x-2

\newline

C)

xy=x-2

\newline

D)

xy=-x+4

Given Differential Equation: Given the differential equation $\frac{dy}{dx} = \frac{y+1}{x^2 - x}$ and the initial condition $x=2$ , $y=1$ . We need to find the particular solution that fits this condition.
Simplify Equation: Simplify the differential equation by factoring the denominator: $\frac{dy}{dx} = \frac{y+1}{(x-1)x}$ .
Apply Initial Condition: Use the initial condition to plug in $x=2$ and $y=1$ into the equation: $\frac{(1+1)}{((2-1)2)} = \frac{2}{2} = 1$ . This confirms that the slope at $x=2$ , $y=1$ is $1$ .
Integrate Differential Equation: To find the particular solution, we need to integrate the differential equation. We can separate variables and integrate: $\int \frac{dy}{y+1} = \int \frac{dx}{x(x-1)}$ .
Exponentiate to Solve for y: Integrate both sides: $\ln|y+1| = \ln|x| - \ln|x-1| + C$ , where $C$ is the integration constant.
Find Integration Constant: Exponentiate both sides to solve for $y$ : $y+1 = C\cdot x/(x-1)$ .
Substitute for Particular Solution: Use the initial condition $(x=2, y=1)$ to find $C$ : $1+1 = C\cdot\frac{2}{(2-1)}$ , so $C = 1$ .
Finalize Solution: Substitute $C$ back into the equation: $y+1 = \frac{x}{x-1}$ . Solve for $y$ : $y = \frac{x}{x-1} - 1 = \frac{x-x+1}{x-1} = \frac{1}{x-1}$ .
Rewrite in Terms of x: Rewrite $y$ in terms of $x$ to match the answer choices: $y = \frac{1}{x-1}$ . Multiply both sides by $x$ : $xy = \frac{x}{x-1}$ .
Simplify the Expression: Simplify the expression: $xy = \frac{x}{x-1} = \frac{x}{x-1} \cdot \frac{x-1}{x-1} = \frac{x}{x-1}$ . This simplifies to $xy = x - 1$ .

More problems from Euler's method

Question

f(x)=x^{3}+6 x^{2}+6 x

c

be the number that satisfies the Mean Value Theorem for

f

on the interval

[-6,0]

\newline

c

\newline

1

\newline

-5

\newline

-4

\newline

-3

\newline

-1

Posted 3 months ago

Question

f(x)=x^{3}+9 x^{2}+13 x

c

be the number that satisfies the Mean Value Theorem for

f

on the interval

-7 \leq x \leq-1

\newline

c

\newline

1

\newline

-6

\newline

-5

\newline

-3

\newline

-2

Posted 3 months ago

Question

h(x)=x^{3}-9 x^{2}+7 x

c

be the number that satisfies the Mean Value Theorem for

h

on the interval

-3 \leq x \leq 6

\newline

c

\newline

1

\newline

-1

\newline

0

\newline

3

\newline

4

Posted 3 months ago

Question

The average cost per meal served at Kiran's restaurant decreases at a rate of

\frac{2400}{q^{2}}

dollars per meal served that month (where

q

is the number of meals served).

\newline

By how many dollars does the average cost per meal decrease between

q=300

q=360

\newline

1

\newline

0

67

\newline

0

81

\newline

1

11

\newline

1

33

Posted 3 months ago

Question

h(x)=-2 x^{3}-7

\newline

The absolute maximum value of

h

over the closed interval

[-3,2]

x

\newline

1

\newline

1

\newline

-2

\newline

2

\newline

-3

Posted 3 months ago

Question

h(x)=x^{3}+6 x^{2}+2

\newline

What is the absolute minimum value of

h

over the closed interval

-6 \leq x \leq 2

\newline

1

\newline

34

\newline

2

\newline

-34

\newline

-2

Posted 3 months ago

Question

g(x)=-2 x^{3}+3 x^{2}+36 x

\newline

The absolute maximum value of

g

over the closed interval

[-3,5]

x

\newline

1

\newline

5

\newline

2

\newline

3

\newline

-3

Posted 3 months ago

Question

h(x)=x^{3}-6 x^{2}+8

\newline

The absolute minimum value of

h

over the closed interval

-1 \leq x \leq 6

x

\newline

1

\newline

-1

\newline

6

\newline

4

\newline

0

Posted 3 months ago

Question

g(x)=x^{3}-12 x+7

\newline

The absolute maximum value of

g

over the closed interval

[-4,5]

x

\newline

1

\newline

5

\newline

-2

\newline

2

\newline

-4

Posted 3 months ago

Question

h(x)=-2 x^{3}-7

\newline

The absolute maximum value of

h

over the closed interval

[-3,2]

x

\newline

1

\newline

-3

\newline

2

\newline

1

\newline

-2

Posted 3 months ago