AI tutor
Full solution
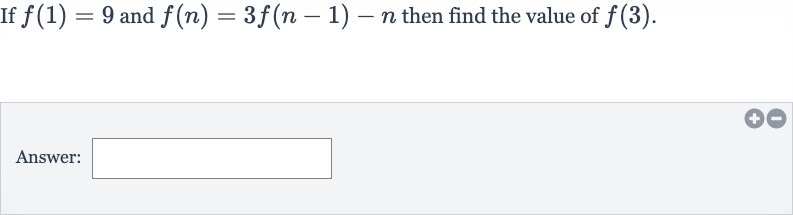
Q. If and then find the value of .Answer:
- Understand the recursive function: Understand the recursive function.The function is defined recursively, meaning that to find , we need to know the value of . We are given that , and we want to find .
- Find using formula: Find the value of using the recursive formula.We use the recursive formula with .Since we know , we substitute that value in.
- Find using formula: Find the value of using the recursive formula.Now we use the recursive formula again with .We found in the previous step, so we substitute that value in.
More problems from Write and solve direct variation equations
Question
In the given equation, is a constant. If the equation has the solutions and , what is the value of ?
Get tutor helpQuestion
In the given equation, is a constant. If the equation has the solutions and , what is the value of ?
Get tutor helpQuestion
In the given equation, is a constant. If the equation has the solutions and , what is the value of ?
Get tutor helpQuestionGet tutor help
QuestionGet tutor help