AI tutor
Full solution
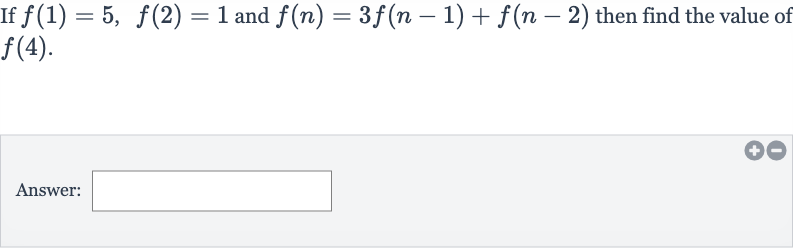
Q. If and then find the value of .Answer:
- Identify Given Information: Identify the given information and the recursive formula.We are given a recursive function , with initial conditions and . We need to find the value of .
- Calculate : Use the recursive formula to find . We know and , so we can calculate using the formula .
- Calculate : Use the recursive formula to find . Now that we have and , we can calculate using the formula .
More problems from Write and solve direct variation equations
Question
In the given equation, is a constant. If the equation has the solutions and , what is the value of ?
Get tutor helpQuestion
In the given equation, is a constant. If the equation has the solutions and , what is the value of ?
Get tutor helpQuestion
In the given equation, is a constant. If the equation has the solutions and , what is the value of ?
Get tutor helpQuestionGet tutor help
QuestionGet tutor help