AI tutor
Full solution
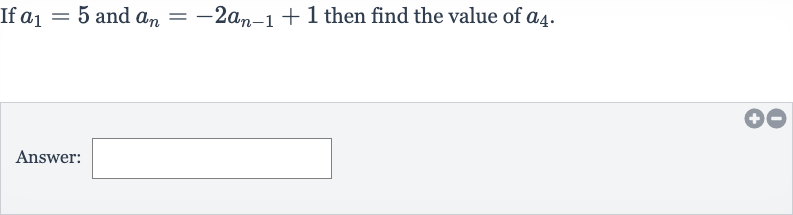
Q. If and then find the value of .Answer:
- Identify first term: Identify the first term in the sequence.We are given that , which is the first term of the sequence.
- Find second term: Use the recursive formula to find the second term, . The recursive formula is . Substitute to find . .
- Find third term: Use the recursive formula to find the third term, . Substitute to find . .
- Find fourth term: Use the recursive formula to find the fourth term, . Substitute to find . .
More problems from Write and solve direct variation equations
Question
In the given equation, is a constant. If the equation has the solutions and , what is the value of ?
Get tutor helpQuestion
In the given equation, is a constant. If the equation has the solutions and , what is the value of ?
Get tutor helpQuestion
In the given equation, is a constant. If the equation has the solutions and , what is the value of ?
Get tutor helpQuestionGet tutor help
QuestionGet tutor help