Full solution
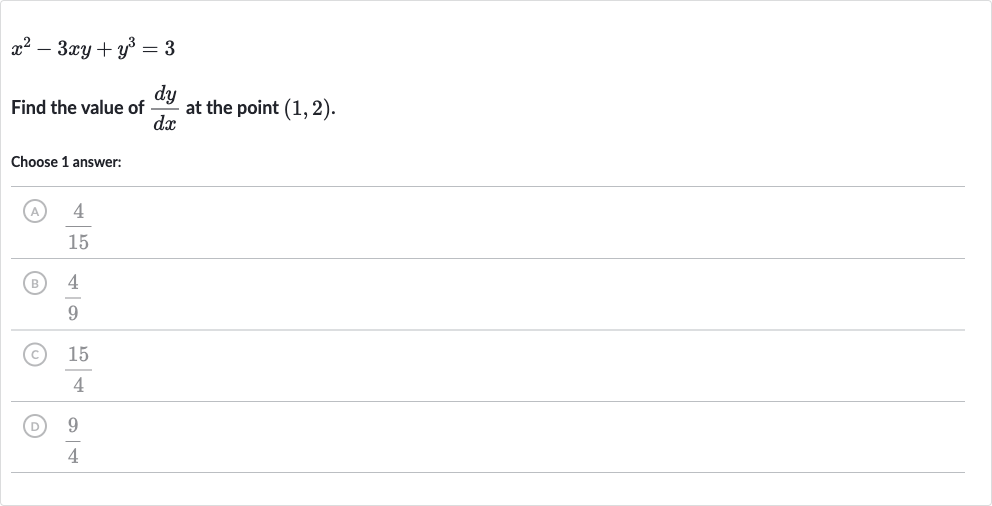
Q. Find the value of at the point .Choose answer:(A) (B) (C) (D)
- Differentiate Equation: Differentiate the given equation with respect to , using implicit differentiation.
- Apply Product Rule: Differentiate each term separately.
- Substitute Values: Apply the product rule to .
- Simplify Equation: Substitute and into the differentiated equation.
- Combine Like Terms: Simplify the equation.
- Solve for : Combine like terms.
- Solve for : Combine like terms. Solve for .
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help