Full solution
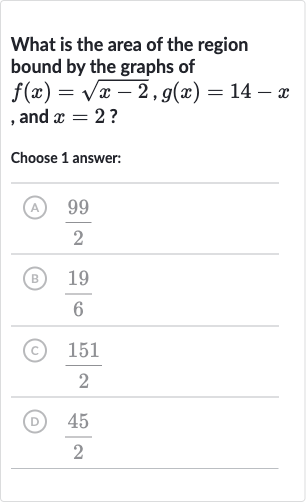
Q. What is the area of the region bound by the graphs of , and ?Choose answer:(A) (B) (C) (D)
- Set up integral limits: To find the area of the region, we need to set up an integral with the appropriate limits of integration. The region is bounded by the graphs of and , and the vertical line . We need to find the points of intersection between and to determine the limits.
- Find points of intersection: Set equal to to find the points of intersection: . Square both sides to eliminate the square root: .
- Simplify and rearrange equation: Simplify the equation: . Expand the right side: .
- Factor quadratic equation: Rearrange the equation to form a quadratic equation: .
- Calculate area using integrals: Factor the quadratic equation: . This gives us the points of intersection and .
- Integrate from to : The area of the region can be found by integrating the difference between and from to , and then from to . The integral is split because is only defined for .
- Evaluate integral at bounds: Set up the integral for the first part from to : .
- Integrate from to : Calculate the integral: .
- Evaluate integral at bounds: Integrate the first part: from to .
- Evaluate integral at bounds: Integrate the first part: from to .Evaluate the first part at the bounds: .
- Evaluate integral at bounds: Integrate the first part: from to .Evaluate the first part at the bounds: .Integrate the second part: . Let , then and when , and when , . The integral becomes .
- Evaluate integral at bounds: Integrate the first part: from to .Evaluate the first part at the bounds: .Integrate the second part: . Let , then and when , and when , . The integral becomes .Calculate the integral: from to .
- Evaluate integral at bounds: Integrate the first part: from to .Evaluate the first part at the bounds: .Integrate the second part: . Let , then and when , and when , . The integral becomes .Calculate the integral: from to .Evaluate the second part at the bounds: .
- Evaluate integral at bounds: Integrate the first part: from to .Evaluate the first part at the bounds: .Integrate the second part: . Let , then and when , and when , . The integral becomes .Calculate the integral: from to .Evaluate the second part at the bounds: .Subtract the second part from the first part to get the area from to : .
- Evaluate integral at bounds: Integrate the first part: from to .Evaluate the first part at the bounds: .Integrate the second part: . Let , then and when , and when , . The integral becomes .Calculate the integral: from to .Evaluate the second part at the bounds: .Subtract the second part from the first part to get the area from to : .Now, set up the integral for the second part from to : .
- Evaluate integral at bounds: Integrate the first part: from to . Evaluate the first part at the bounds: . Integrate the second part: . Let , then and when , and when , . The integral becomes . Calculate the integral: from to . Evaluate the second part at the bounds: . Subtract the second part from the first part to get the area from to : . Now, set up the integral for the second part from to : . Calculate the integral: from to .
- Evaluate integral at bounds: Integrate the first part: from to .Evaluate the first part at the bounds: .Integrate the second part: . Let , then and when , and when , . The integral becomes .Calculate the integral: from to .Evaluate the second part at the bounds: .Subtract the second part from the first part to get the area from to : .Now, set up the integral for the second part from to : .Calculate the integral: from to .Evaluate the integral at the bounds: .
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help