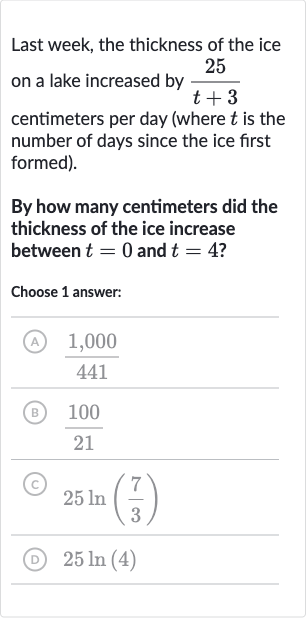
Last week, the thickness of the ice on a lake increased by (25)/(t+3) centimeters per day (where t is the number of days since the ice first formed). By how many centimeters did the thickness of the ice increase between t=0 and t=4 ? Choose 1 answer: (A) (1,000)/(441) (B) (100)/(21) (C) 25 ln((7)/(3)) (D) 25 ln(4)

Question

Last week, the thickness of the ice on a lake increased by  (25)/(t+3) centimeters per day (where  t is the number of days since the ice first formed). By how many centimeters did the thickness of the ice increase between  t=0 and  t=4 ? Choose 1 answer: (A)  (1,000)/(441) (B)  (100)/(21) (C)  25 ln((7)/(3)) (D)  25 ln(4)

Bytelearn · Accepted Answer

Integrate Rate of Increase: To find the total increase in thickness over a period of time, we need to integrate the rate of increase with respect to time from the starting time to the ending time.Given Rate Function: The rate of increase in thickness is given by the function f(t) = (25)/(t+3) centimeters per day. We need to integrate this function from t=0 to t=4.Calculate Integral: The integral of f(t) from t=0 to t=4 is ∫(25)/(t+3) dt from 0 to 4.Apply Logarithm Rule: To integrate f(t), we recognize that the integral of 1/(t+3) is the natural logarithm of the absolute value of (t+3). Therefore, the integral of (25)/(t+3) is 25 times the natural logarithm of the absolute value of (t+3).Calculate Definite Integral: We calculate the definite integral: 25 * [ln|t+3|] from 0 to 4.Evaluate Limits: Plugging in the limits of integration, we get 25 * [ln|4+3| - ln|0+3|] = 25 * [ln(7) - ln(3)].Combine Logarithms: We use the properties of logarithms to combine the terms: ln(7) - ln(3) = ln(7/3).Final Result: The final result is 25 * ln(7/3).Compare with Answer: Comparing the final result with the answer choices, we see that it matches with option (C) 25 ln((7)/(3)).

Full solution

More problems from Operations with rational exponents

Related topics