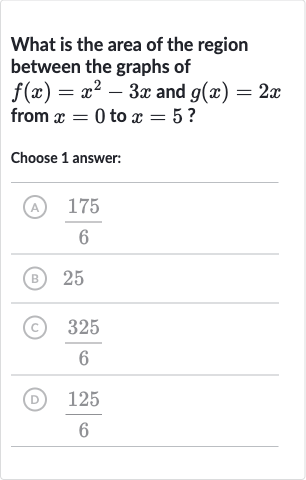
What is the area of the region between the graphs of f(x)=x^(2)-3x and g(x)=2x from x=0 to x=5 ? Choose 1 answer: (A) (175)/(6) (B) 25 (C) (325)/(6) (D) (125)/(6)

Question

What is the area of the region between the graphs of  f(x)=x^(2)-3x and  g(x)=2x from  x=0 to  x=5 ? Choose 1 answer: (A)  (175)/(6) (B) 25 (C)  (325)/(6) (D)  (125)/(6)

Bytelearn · Accepted Answer

Set up integral: Set up the integral to find the area between the two curves. The area A between the two curves from x = a to x = b is given by the integral of the top function minus the bottom function, from a to b. In this case, we need to determine which function is on top (greater y-value) for the interval from x = 0 to x = 5.Compare functions at point: Compare the functions at a point to determine which is on top. Let's evaluate both functions at a point within the interval, say x = 1. f(1) = 1^2 - 3(1) = 1 - 3 = -2 g(1) = 2(1) = 2 Since g(1) > f(1), we can assume that g(x) is the top function for the interval. However, we should verify this for the entire interval to be certain.Verify functions for interval: Verify that g(x) is above f(x) for the entire interval from x = 0 to x = 5. We can do this by finding the points of intersection, if any, between f(x) and g(x) within the interval. Set f(x) equal to g(x) and solve for x: x^2 - 3x = 2x x^2 - 5x = 0 x(x - 5) = 0 x = 0 or x = 5 The functions intersect at the endpoints of the interval, so g(x) is indeed above f(x) for the entire interval from x = 0 to x = 5.Set up definite integral: Set up the definite integral to find the area. The area A is given by the integral from 0 to 5 of (g(x) - f(x)) dx. A = ∫ from 0 to 5 of (2x - (x^2 - 3x)) dx A = ∫ from 0 to 5 of (-x^2 + 5x) dxCalculate integral: Calculate the integral. A = ∫ from 0 to 5 of (-x^2 + 5x) dx To integrate, we find the antiderivative: A = [(-1/3)x^3 + (5/2)x^2] from 0 to 5Evaluate antiderivative: Evaluate the antiderivative at the upper and lower limits of integration. A = [(-1/3)(5)^3 + (5/2)(5)^2] - [(-1/3)(0)^3 + (5/2)(0)^2] A = [(-1/3)(125) + (5/2)(25)] - [0 + 0] A = [(-125/3) + (125/2)]Simplify expression: Simplify the expression to find the area. A = [(-125/3) + (125/2)] To combine the fractions, find a common denominator, which is 6: A = [(-250/6) + (375/6)] A = (125/6)Check for errors: Check for any mathematical errors in the calculations. Re-evaluate the antiderivative and the arithmetic to ensure there are no errors.

What is the area of the region between the graphs of $f(x)=x^{2}-3 x$ and $g(x)=2 x$ from $x=0$ to $x=5$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{175}{6}$ $\newline$ (B) $25$ $\newline$ (C) $\frac{325}{6}$ $\newline$ (D) $\frac{125}{6}$

Full solution

More problems from Operations with rational exponents

Related topics