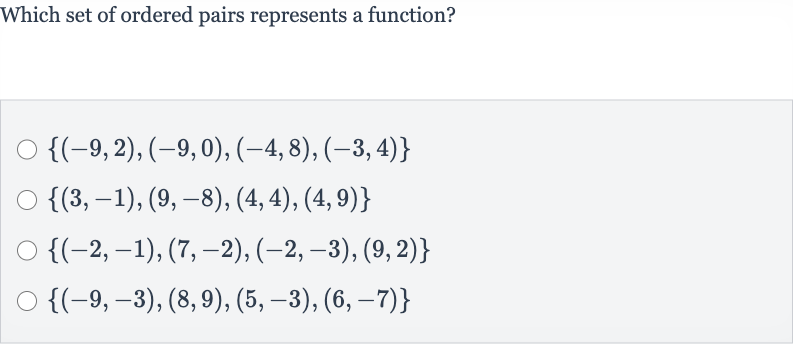Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which set of ordered pairs represents a function? {(-9,2),(-9,0),(-4,8),(-3,4)} {(3,-1),(9,-8),(4,4),(4,9)} {(-2,-1),(7,-2),(-2,-3),(9,2)} {(-9,-3),(8,9),(5,-3),(6,-7)}

Which set of ordered pairs represents a function?\newline{(−9,2),(−9,0),(−4,8),(−3,4)} \{(-9,2),(-9,0),(-4,8),(-3,4)\} \newline{(3,−1),(9,−8),(4,4),(4,9)} \{(3,-1),(9,-8),(4,4),(4,9)\} \newline{(−2,−1),(7,−2),(−2,−3),(9,2)} \{(-2,-1),(7,-2),(-2,-3),(9,2)\} \newline{(−9,−3),(8,9),(5,−3),(6,−7)} \{(-9,-3),(8,9),(5,-3),(6,-7)\}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Is (x, y) a solution to the system of equations?right chevron icon

Full solution

Q. Which set of ordered pairs represents a function?\newline{(−9,2),(−9,0),(−4,8),(−3,4)} \{(-9,2),(-9,0),(-4,8),(-3,4)\} \newline{(3,−1),(9,−8),(4,4),(4,9)} \{(3,-1),(9,-8),(4,4),(4,9)\} \newline{(−2,−1),(7,−2),(−2,−3),(9,2)} \{(-2,-1),(7,-2),(-2,-3),(9,2)\} \newline{(−9,−3),(8,9),(5,−3),(6,−7)} \{(-9,-3),(8,9),(5,-3),(6,-7)\}
  1. Check for Function: A set of ordered pairs represents a function if each input (first component of each ordered pair) corresponds to exactly one output (second component). We will check each set of ordered pairs to see if any input value is repeated with different output values.
  2. Set 11 Analysis: Examine the first set (−9,2),(−9,0),(−4,8),(−3,4){(-9,2),(-9,0),(-4,8),(-3,4)}. The input value −9-9 corresponds to two different output values, 22 and 00. This violates the definition of a function, so this set does not represent a function.
  3. Set 22 Analysis: Examine the second set (3,−1),(9,−8),(4,4),(4,9){(3,-1),(9,-8),(4,4),(4,9)}. The input value 44 corresponds to two different output values, 44 and 99. This also violates the definition of a function, so this set does not represent a function.
  4. Set 33 Analysis: Examine the third set (−2,−1),(7,−2),(−2,−3),(9,2){(-2,-1),(7,-2),(-2,-3),(9,2)}. The input value −2-2 corresponds to two different output values, −1-1 and −3-3. This again violates the definition of a function, so this set does not represent a function.
  5. Set 44 Analysis: Examine the fourth set {(−9,−3),(8,9),(5,−3),(6,−7)}\{(-9,-3),(8,9),(5,-3),(6,-7)\}. Each input value corresponds to exactly one output value. There are no repeated input values with different outputs. This set satisfies the definition of a function.
  6. Identify Function Set: Since the 4th4^{\text{th}} set is the only one where each input has a unique output, it is the set that represents a function.

More problems from Is (x, y) a solution to the system of equations?

Question
Solve using substitution. 5x−2y=−7 5x - 2y = -7 x=−5 x = -5 (_,_)
Get tutor helpright-arrow

Posted 2 months ago

Question
Is (1,1)(1,1) a solution to this system of equations? \newline4x+10y=144x + 10y = 14\newlinex+6y=7x + 6y = 7\newlineChoices:\newline(A) yes \newline(B) no
Get tutor helpright-arrow

Posted 2 months ago

Question
Which describes the system of equations below?\newliney=–3x+9y = –3x + 9 \newliney=–3x+9y = –3x + 9 \newlineChoices:\newline(A) consistent and independent\text{(A) consistent and independent} \newline(B) consistent and dependent\text{(B) consistent and dependent} \newline(C) inconsistent\text{(C) inconsistent}
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve using elimination. \newline7x−8y=−17 7x - 8y = -17 \newline −7x+3y=2 -7x + 3y = 2 \newline (____,____)(\_\_\_\_, \_\_\_\_)
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. \newlinex=−2 x = -2 \newline−2x+2y=−8 -2x + 2y = -8 \newline(____,____)(\_\_\_\_, \_\_\_\_)
Get tutor helpright-arrow

Posted 2 months ago

Question
Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.\newlineAt a community barbecue, Mrs. Wilkerson and Mr. Hogan are buying dinner for their families. Mrs. Wilkerson purchases 33 hot dog meals and 33 hamburger meals, paying a total of $36\$36. Mr. Hogan buys 11 hot dog meal and 33 hamburger meals, spending $26\$26 in all. How much do the meals cost?\newlineHot dog meals cost $\$_______ each, and hamburger meals cost $\$________ each.
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve the system of equations by substitution.\newline−3x−y−3z=−11-3x - y - 3z = -11\newlinez=5z = 5\newlinex−y+3z=19x - y + 3z = 19\newline(____.____,____)
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve the system of equations by elimination.\newlinex−3y−2z=10 x - 3y - 2z = 10 \newline3x+2y+2z=14 3x + 2y + 2z = 14 \newline2x−3y−2z=16 2x - 3y - 2z = 16 \newline(_,_,_)(\_,\_,\_)
Get tutor helpright-arrow

Posted 1 month ago

Question
Solve the system of equations.\newliney=x2+36x+3 y = x^2 + 36x + 3 \newliney=22x−37 y = 22x - 37 \newlineWrite the coordinates in exact form. Simplify all fractions and radicals.\newline(_,_)(\_,\_)\newline(_,_)(\_,\_)
Get tutor helpright-arrow

Posted 1 month ago

Question
Solve the system of equations.\newliney=−x−24 y = -x - 24 \newlinex2+y2=488 x^2 + y^2 = 488 \newlineWrite the coordinates in exact form. Simplify all fractions and radicals.\newline(_,_) (\_,\_) \newline(_,_) (\_,\_)
Get tutor helpright-arrow

Posted 2 months ago

View all (85)