Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which of the following functions are continuous for all real numbers?

g(x)=ln(x)

f(x)=(1)/(x)
Choose 1 answer:
A)
g only
(B)
f only
(C) Both
g and
f
(D) Neither
g nor
f

Which of the following functions are continuous for all real numbers? $\newline$ $g(x)=\ln(x)$ $\newline$ $f(x)=\frac{1}{x}$ $\newline$ Choose $1$ answer: $\newline$ A) $g$ only $\newline$ (B) $f$ only $\newline$ (C) Both $g$ and $f$ $\newline$ (D) Neither $g$ nor $f$

View step-by-step help

View step-by-step help

Intermediate Value Theorem

Full solution

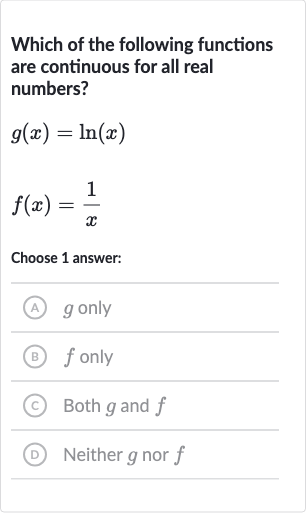
Q. Which of the following functions are continuous for all real numbers?

\newline

g(x)=\ln(x)

\newline

f(x)=\frac{1}{x}

\newline

Choose

1

answer:

\newline

A)

g

only

\newline

(B)

f

only

\newline

(C) Both

g

and

f

\newline

(D) Neither

g

nor

f

Question Prompt: Question prompt: Determine which of the given functions, $g(x) = \ln(x)$ and $f(x) = \frac{1}{x}$ , are continuous for all real numbers.
Analyze $g(x) = \ln(x)$ : Analyze the function $g(x) = \ln(x)$ . The natural logarithm function $\ln(x)$ is defined only for $x > 0$ . Therefore, $g(x)$ is not continuous for all real numbers because it is not defined for $x \leq 0$ .
Analyze $f(x) = \frac{1}{x}$ : Analyze the function $f(x) = \frac{1}{x}$ . The function $\frac{1}{x}$ is defined for all real numbers except $x = 0$ , where it has a vertical asymptote. Therefore, $f(x)$ is not continuous at $x = 0$ and thus not continuous for all real numbers.
Conclusion: Since neither $g(x) = \ln(x)$ nor $f(x) = \frac{1}{x}$ is continuous for all real numbers, the correct answer is (D) Neither $g$ nor $f$ .

More problems from Intermediate Value Theorem

Question

Which of the following functions are continuous for all real numbers?

\newline

g(x)=\ln (x)

\newline

f(x)=\frac{1}{x}

\newline

1

\newline

g

\newline

f

\newline

g

f

\newline

g

f

Posted 3 months ago

Question

\newline

f(x)=\left\{\begin{array}{ll} \ln (-x)+3 & \text { for } x<-3 \\ \ln (-x+3) & \text { for }-3 \leq x<3 \end{array}\right.

\newline

f

x=-3

\newline

1

\newline

\newline

\mathrm{No}

Posted 2 months ago

Question

\newline

f(x)=\left\{\begin{array}{ll}\ln (x) & \text { for } 0<x \leq 2 \\ x^{2} \ln (2) & \text { for } x>2\end{array}\right.

\newline

f

x=2

\newline

1

\newline

\newline

\mathrm{No}

Posted 3 months ago

Question

\newline

g(x)=\left\{\begin{array}{ll} \frac{1}{\cos (x)} & \text { for }-\frac{\pi}{2}<x<0 \\ \cos (x+\pi) & \text { for } x \geq 0 \end{array}\right.

\newline

g

x=0

\newline

1

\newline

\newline

Posted 3 months ago

Question

\newline

h(x)=\left\{\begin{array}{ll} 2^{x-1} & \text { for } x<1 \\ 2^{1-x} & \text { for } x \geq 1 \end{array}\right.

\newline

h

x=1

\newline

1

\newline

\newline

Posted 3 months ago

Question

\newline

g(x)=\left\{\begin{array}{ll} (x-2)^{2} & \text { for } x \leq 2 \\ 2-x^{2} & \text { for } x>2 \end{array}\right.

\newline

g

x=2

\newline

1

\newline

\newline

\mathrm{No}

Posted 3 months ago

Question

\newline

g(x)=\left\{\begin{array}{ll} e^{x} & \text { for } x \leq-1 \\ -e^{-x} & \text { for } x>-1 \end{array}\right.

\newline

g

x=-1

\newline

1

\newline

\newline

Posted 3 months ago

Question

\newline

h(x)=\left\{\begin{array}{ll} e^{2 x} & \text { for } x<0 \\ e^{5 x} & \text { for } x \geq 0 \end{array}\right.

\newline

h

x=0

\newline

1

\newline

\newline

Posted 3 months ago

Question

\newline

h(x)=\left\{\begin{array}{cl}\frac{6}{x+5} & \text { for }-5<x<-3 \\ x^{2}-6 & \text { for } x \geq-3\end{array}\right.

\newline

h

x=-3

\newline

1

\newline

\newline

Posted 3 months ago

Question

\newline

g(x)=\left\{\begin{array}{ll}\sin (x) & \text { for } x<0 \\ x^{2} & \text { for } x \geq 0\end{array}\right.

\newline

g

x=0

\newline

1

\newline

\newline

Posted 3 months ago