Full solution
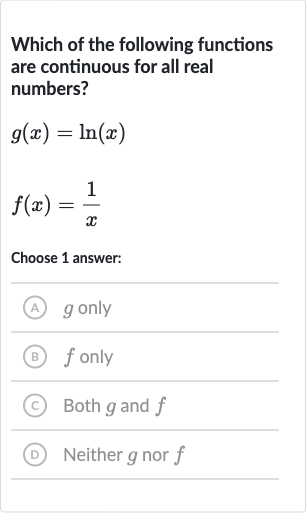
Q. Which of the following functions are continuous for all real numbers?Choose answer:A) only(B) only(C) Both and D Neither nor
- Consider the domain: To determine if is continuous for all real numbers, we need to consider the domain of the natural logarithm function.
- Natural logarithm function: The natural logarithm function is defined only for x > 0. Therefore, is not continuous for all real numbers because it is not defined for .
- Consider the domain: To determine if is continuous for all real numbers, we need to consider the domain of the reciprocal function.
- Reciprocal function: The function is defined for all real numbers except , where the function has a vertical asymptote and is not defined.
- Neither g nor f: Since neither nor is continuous for all real numbers, the correct answer is D) Neither nor .