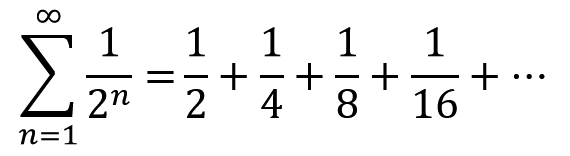AI tutor
Full solution
Q. Does the series converge or diverge?
- Given series: We are given the infinite geometric series . To find the sum of an infinite geometric series, we use the formula , where is the first term and is the common ratio.In our case, the first term and the common ratio .
- Formula application: Now we apply the formula for the sum of an infinite geometric series:.
- Simplify expression: Simplify the expression:.
- Final result: The sum of the infinite series is .