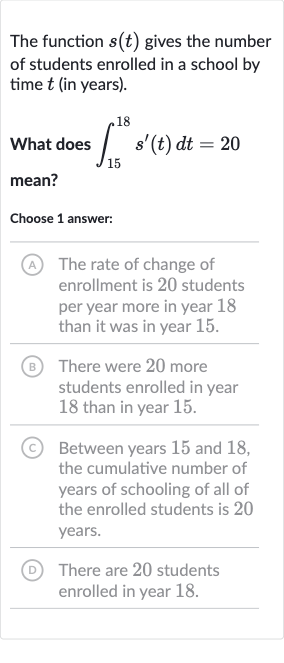
The function s(t) gives the number of students enrolled in a school by time t (in years). What does int_(15)^(18)s^(')(t)dt=20 mean? Choose 1 answer: (A) The rate of change of enrollment is 20 students per year more in year 18 than it was in year 15. (B) There were 20 more students enrolled in year 18 than in year 15 . (C) Between years 15 and 18, the cumulative number of years of schooling of all of the enrolled students is 20 years. (D) There are 20 students enrolled in year 18.

Question

The function  s(t) gives the number of students enrolled in a school by time  t (in years). What does  int_(15)^(18)s^(')(t)dt=20 mean? Choose 1 answer: (A) The rate of change of enrollment is 20 students per year more in year 18 than it was in year 15. (B) There were 20 more students enrolled in year 18 than in year 15 . (C) Between years 15 and 18, the cumulative number of years of schooling of all of the enrolled students is 20 years. (D) There are 20 students enrolled in year 18.

Bytelearn · Accepted Answer

Concept Explanation: The integral of the derivative of a function over an interval gives the net change in the function's value over that interval. In this case, the function s(t) represents the number of students enrolled in a school at time t. The derivative s'(t) represents the rate of change of the number of students with respect to time.Integral Calculation: By integrating s'(t) from 15 to 18, we are finding the total change in the number of students from year 15 to year 18. Since the integral is equal to 20, this means that there is a net increase of 20 students over this time period.Analysis of Answer Choices: Now we need to match this interpretation with the correct answer choice. The integral does not give us information about the rate of change per year, so option (A) is incorrect. Option (C) is incorrect because the integral does not represent cumulative years of schooling. Option (D) is incorrect because the integral does not tell us the total number of students enrolled in year 18, but rather the change in enrollment between years 15 and 18.Correct Interpretation: The correct interpretation is that there were 20 more students enrolled in year 18 than in year 15, which corresponds to option (B). This is because the integral of the rate of change of enrollment (s'(t)) from year 15 to year 18 equals 20, indicating the net increase in enrollment over that period.

Full solution

More problems from Evaluate definite integrals using the power rule

Related topics