AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
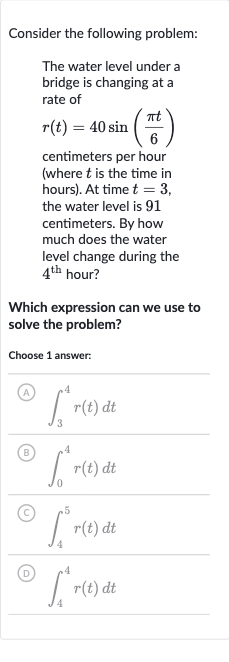
Consider the following problem:The water level under a bridge is changing at a rate of centimeters per hour (where is the time in hours). At time , the water level is centimeters. By how much does the water level change during the hour?Which expression can we use to solve the problem?Choose answer:(A) (B) (C) (D)
Full solution
Q. Consider the following problem:The water level under a bridge is changing at a rate of centimeters per hour (where is the time in hours). At time , the water level is centimeters. By how much does the water level change during the hour?Which expression can we use to solve the problem?Choose answer:(A) (B) (C) (D)
- Integrate rate of change: To find the change in water level during the hour, we need to integrate the rate of change function, , from the start of the hour to the end of the hour.
- Identify time interval: The hour starts at and ends at . Therefore, we need to evaluate the integral of from to .
- Evaluate integral expression: The correct expression to use for solving the problem is the integral of from to , which is option (A) .
