Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Evaluate the integral. int-2x^(3)cos(3x)dx Answer:

Evaluate the integral.\newline∫−2x3cos⁡(3x)dx \int-2 x^{3} \cos (3 x) d x \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Evaluate definite integrals using the chain ruleright chevron icon

Full solution

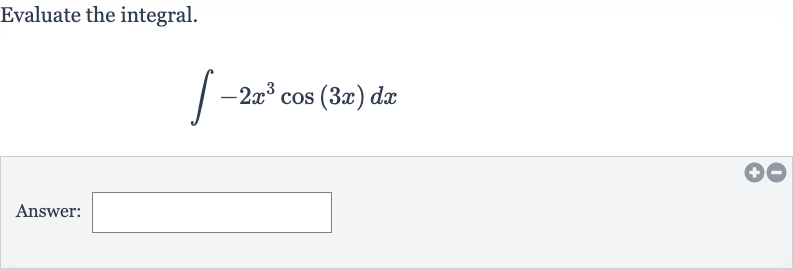
Q. Evaluate the integral.\newline∫−2x3cos⁡(3x)dx \int-2 x^{3} \cos (3 x) d x \newlineAnswer:
  1. Identify Integral: Identify the integral that needs to be evaluated.\newlineWe need to evaluate the integral of the function −2x3cos⁡(3x)-2x^3 \cos(3x) with respect to xx. This is an integration problem that requires the use of integration by parts, which is based on the formula ∫u dv=uv−∫v du\int u \, dv = uv - \int v \, du.
  2. Choose uu and dvdv: Choose uu and dvdv for integration by parts.\newlineLet u=−2x3u = -2x^3, which means du=−6x2dxdu = -6x^2 dx after differentiation.\newlineLet dv=cos⁡(3x)dxdv = \cos(3x) dx, which means v=(1/3)sin⁡(3x)v = (1/3)\sin(3x) after integration.
  3. Apply Integration by Parts: Apply the integration by parts formula.\newlineUsing the integration by parts formula, we have:\newline∫−2x3cos⁡(3x) dx=uv−∫v du\int -2x^3 \cos(3x) \, dx = uv - \int v \, du\newline= (−2x3)(13)sin⁡(3x)−∫(13)sin⁡(3x)(−6x2 dx)(-2x^3)(\frac{1}{3})\sin(3x) - \int (\frac{1}{3})\sin(3x)(-6x^2 \, dx)\newline= (-\frac{\(2\)}{\(3\)})x^\(3 \sin(33x) + 22 \int x^22 \sin(33x) \, dx)
  4. Apply Integration by Parts Again: Apply integration by parts again to the remaining integral.\newlineWe need to apply integration by parts again to the integral ∫x2sin⁡(3x) dx\int x^2 \sin(3x) \, dx.\newlineLet u=x2u = x^2, which means du=2x dxdu = 2x \, dx after differentiation.\newlineLet dv=sin⁡(3x) dxdv = \sin(3x) \, dx, which means v=−(1/3)cos⁡(3x)v = -(1/3)\cos(3x) after integration.
  5. Apply Integration by Parts Formula: Apply the integration by parts formula to the new integral.\newlineUsing the integration by parts formula again, we have:\newline∫x2sin⁡(3x) dx=uv−∫v du\int x^2 \sin(3x) \, dx = uv - \int v \, du\newline=x2(−13)cos⁡(3x)−∫(−13)cos⁡(3x)(2x dx)= x^2(-\frac{1}{3})\cos(3x) - \int(-\frac{1}{3})\cos(3x)(2x \, dx)\newline=−(13)x2cos⁡(3x)+(23)∫xcos⁡(3x) dx= -(\frac{1}{3})x^2 \cos(3x) + (\frac{2}{3}) \int x \cos(3x) \, dx
  6. Apply Integration by Parts Again: Apply integration by parts one more time to the remaining integral.\newlineWe need to apply integration by parts one more time to the integral ∫xcos⁡(3x) dx\int x \cos(3x) \, dx.\newlineLet u=xu = x, which means du=dxdu = dx after differentiation.\newlineLet dv=cos⁡(3x) dxdv = \cos(3x) \, dx, which means v=(13)sin⁡(3x)v = (\frac{1}{3})\sin(3x) after integration.
  7. Apply Integration by Parts Formula: Apply the integration by parts formula to the final integral.\newlineUsing the integration by parts formula one more time, we have:\newline∫xcos⁡(3x) dx=uv−∫v du\int x \cos(3x) \, dx = uv - \int v \, du\newline= x(13)sin⁡(3x)−∫(13)sin⁡(3x) dxx(\frac{1}{3})\sin(3x) - \int(\frac{1}{3})\sin(3x) \, dx\newline= (13)xsin⁡(3x)−(19)cos⁡(3x)+C(\frac{1}{3})x \sin(3x) - (\frac{1}{9})\cos(3x) + C
  8. Combine for Final Answer: Combine all parts to get the final answer.\newlineNow we combine all parts to get the final answer for the original integral:\newline∫−2x3cos⁡(3x) dx=(−23)x3sin⁡(3x)+2[−(13)x2cos⁡(3x)+(23)((13)xsin⁡(3x)−(19)cos⁡(3x))]+C\int -2x^3 \cos(3x) \, dx = \left(-\frac{2}{3}\right)x^3 \sin(3x) + 2\left[-\left(\frac{1}{3}\right)x^2 \cos(3x) + \left(\frac{2}{3}\right)\left(\left(\frac{1}{3}\right)x \sin(3x) - \left(\frac{1}{9}\right)\cos(3x)\right)\right] + C\newlineSimplify the expression:\newline=(−23)x3sin⁡(3x)−(23)x2cos⁡(3x)+(49)xsin⁡(3x)−(427)cos⁡(3x)+C= \left(-\frac{2}{3}\right)x^3 \sin(3x) - \left(\frac{2}{3}\right)x^2 \cos(3x) + \left(\frac{4}{9}\right)x \sin(3x) - \left(\frac{4}{27}\right)\cos(3x) + C

More problems from Evaluate definite integrals using the chain rule

Question
Consider the following problem:\newlineThe water level under a bridge is changing at a rate of r(t)=40sin⁡(πt6) r(t)=40 \sin \left(\frac{\pi t}{6}\right) centimeters per hour (where t t is the time in hours). At time t=3 t=3 , the water level is 9191 centimeters. By how much does the water level change during the 4th  4^{\text {th }} hour?\newlineWhich expression can we use to solve the problem?\newlineChoose 11 answer:\newline(A) ∫34r(t)dt \int_{3}^{4} r(t) d t \newline(B) ∫04r(t)dt \int_{0}^{4} r(t) d t \newline(C) ∫45r(t)dt \int_{4}^{5} r(t) d t \newline(D) ∫44r(t)dt \int_{4}^{4} r(t) d t
Get tutor helpright-arrow

Posted 8 months ago

Question
The function s(t) s(t) gives the number of students enrolled in a school by time t t (in years).\newlineWhat does ∫1518s′(t)dt=20 \int_{15}^{18} s^{\prime}(t) d t=20 mean?\newlineChoose 11 answer:\newline(A) The rate of change of enrollment is 2020 students per year more in year 1818 than it was in year 1515.\newline(B) There were 2020 more students enrolled in year 1818 than in year 1515 .\newline(C) Between years 1515 and 1818, the cumulative number of years of schooling of all of the enrolled students is 2020 years.\newline(D) There are 2020 students enrolled in year 1818.
Get tutor helpright-arrow

Posted 7 months ago

Question
A water tank is filled at a rate of r(t) r(t) liters per minute (where t t is the time in minutes).\newlineWhat does ∫17r′(t)dt \int_{1}^{7} r^{\prime}(t) d t represent?\newlineChoose 11 answer:\newline(A) The rate at which the tank was filled at t=7 t=7 .\newlineB) The average rate of filling between t=1 t=1 and t=7 t=7 .\newline(C) The change in the rate of filling between t=1 t=1 and t=7 t=7 .\newline(D) The amount of water filled between t=1 t=1 and t=7 t=7 .
Get tutor helpright-arrow

Posted 8 months ago

Question
The base of a solid is the region enclosed by the graphs of y=sin⁡(x) y=\sin (x) and y=4−x y=4-\sqrt{x} , between x=2 x=2 and x=7 x=7 .\newlineCross sections of the solid perpendicular to the x x -axis are rectangles whose height is 2x 2 x .\newlineWhich one of the definite integrals gives the volume of the solid?\newlineChoose 11 answer:\newline(A) ∫27[(4−x)2−sin⁡2(x)]dx \int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x \newline(B) ∫27[sin⁡(x)+x−4]⋅2xdx \int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x \newline(C) ∫27[sin⁡2(x)−(4−x)2]dx \int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x \newline(D) ∫27[4−x−sin⁡(x)]⋅2xdx \int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate the integral.\newline∫−4x233xdx \int-4 x^{2} 3^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−4x2e4xdx \int-4 x^{2} e^{4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
∑n=1∞3nn2n!\sum_{n=1}^{\infty}\frac{3^{n}n^{2}}{n!}
Get tutor helpright-arrow

Posted 8 months ago

Question
f)lim⁡n→+∞[2n+(35)n] f) \lim_{n \to +\infty}\left[\frac{2}{n}+\left(\frac{3}{5}\right)^n\right]
Get tutor helpright-arrow

Posted 8 months ago

Question
∫1cos⁡(x)2 dx\int \frac{1}{\cos(x)^{2}}\,dx
Get tutor helpright-arrow

Posted 8 months ago

Question
You pick a card at random, put it back, and then pick another card at random.\newline44\newline55\newline66\newline77\newlineWhat is the probability of picking a number greater than 55 and then picking a 44 ?\newlineWrite your answer as a percentage.
Get tutor helpright-arrow

Posted 1 month ago

View all (198)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant