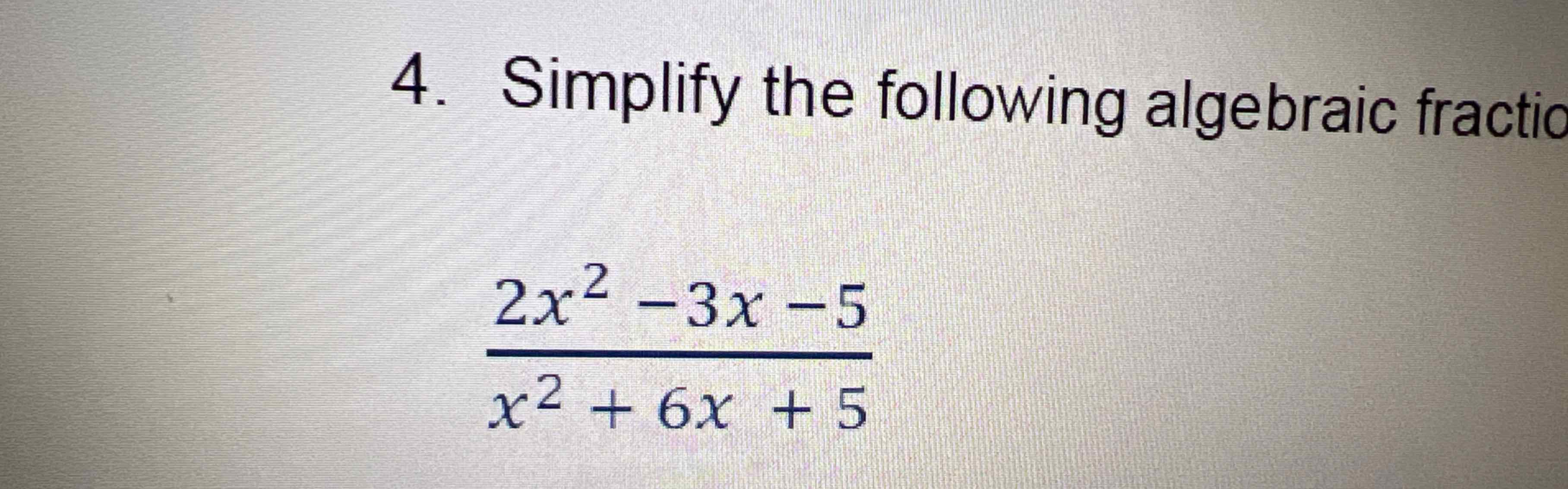Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify the following algebraic fraction: (2x^(2)-3x-5)/(x^(2)+6x+5)

Simplify the following algebraic fraction:\newline2x2−3x−5x2+6x+5\frac{2x^{2}-3x-5}{x^{2}+6x+5}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Evaluate definite integrals using the chain ruleright chevron icon

Full solution

Q. Simplify the following algebraic fraction:\newline2x2−3x−5x2+6x+5\frac{2x^{2}-3x-5}{x^{2}+6x+5}
  1. Factorize Numerator and Denominator: Factorize the numerator and denominator of the fraction.\newlineNumerator: 2x2−3x−52x^2 - 3x - 5. We look for two numbers that multiply to 2×−5=−102 \times -5 = -10 and add to −3-3. These numbers are −5-5 and 22.\newlineSo, 2x2−3x−5=(2x+1)(x−5)2x^2 - 3x - 5 = (2x + 1)(x - 5).\newlineDenominator: x2+6x+5x^2 + 6x + 5. We look for two numbers that multiply to 1×5=51 \times 5 = 5 and add to 66. These numbers are 11 and 55.\newlineSo, x2+6x+5=(x+1)(x+5)x^2 + 6x + 5 = (x + 1)(x + 5).
  2. Simplify by Canceling Common Factors: Simplify the fraction by canceling common factors.\newline(2x+1)(x−5)(x+1)(x+5) \frac{(2x + 1)(x - 5)}{(x + 1)(x + 5)} \newlineWe can cancel the (x+5)(x + 5) terms in the numerator and denominator.
  3. Write Simplified Expression: Write the simplified expression.\newline2x+1x+1 \frac{2x + 1}{x + 1} \newlineThis is the simplified form of the given algebraic fraction.

More problems from Evaluate definite integrals using the chain rule

Question
Consider the following problem:\newlineThe water level under a bridge is changing at a rate of r(t)=40sin⁡(πt6) r(t)=40 \sin \left(\frac{\pi t}{6}\right) centimeters per hour (where t t is the time in hours). At time t=3 t=3 , the water level is 9191 centimeters. By how much does the water level change during the 4th  4^{\text {th }} hour?\newlineWhich expression can we use to solve the problem?\newlineChoose 11 answer:\newline(A) ∫34r(t)dt \int_{3}^{4} r(t) d t \newline(B) ∫04r(t)dt \int_{0}^{4} r(t) d t \newline(C) ∫45r(t)dt \int_{4}^{5} r(t) d t \newline(D) ∫44r(t)dt \int_{4}^{4} r(t) d t
Get tutor helpright-arrow

Posted 8 months ago

Question
The function s(t) s(t) gives the number of students enrolled in a school by time t t (in years).\newlineWhat does ∫1518s′(t)dt=20 \int_{15}^{18} s^{\prime}(t) d t=20 mean?\newlineChoose 11 answer:\newline(A) The rate of change of enrollment is 2020 students per year more in year 1818 than it was in year 1515.\newline(B) There were 2020 more students enrolled in year 1818 than in year 1515 .\newline(C) Between years 1515 and 1818, the cumulative number of years of schooling of all of the enrolled students is 2020 years.\newline(D) There are 2020 students enrolled in year 1818.
Get tutor helpright-arrow

Posted 7 months ago

Question
A water tank is filled at a rate of r(t) r(t) liters per minute (where t t is the time in minutes).\newlineWhat does ∫17r′(t)dt \int_{1}^{7} r^{\prime}(t) d t represent?\newlineChoose 11 answer:\newline(A) The rate at which the tank was filled at t=7 t=7 .\newlineB) The average rate of filling between t=1 t=1 and t=7 t=7 .\newline(C) The change in the rate of filling between t=1 t=1 and t=7 t=7 .\newline(D) The amount of water filled between t=1 t=1 and t=7 t=7 .
Get tutor helpright-arrow

Posted 8 months ago

Question
The base of a solid is the region enclosed by the graphs of y=sin⁡(x) y=\sin (x) and y=4−x y=4-\sqrt{x} , between x=2 x=2 and x=7 x=7 .\newlineCross sections of the solid perpendicular to the x x -axis are rectangles whose height is 2x 2 x .\newlineWhich one of the definite integrals gives the volume of the solid?\newlineChoose 11 answer:\newline(A) ∫27[(4−x)2−sin⁡2(x)]dx \int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x \newline(B) ∫27[sin⁡(x)+x−4]⋅2xdx \int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x \newline(C) ∫27[sin⁡2(x)−(4−x)2]dx \int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x \newline(D) ∫27[4−x−sin⁡(x)]⋅2xdx \int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate the integral.\newline∫−2x3cos⁡(3x)dx \int-2 x^{3} \cos (3 x) d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−4x233xdx \int-4 x^{2} 3^{3 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
Evaluate the integral.\newline∫−4x2e4xdx \int-4 x^{2} e^{4 x} d x \newlineAnswer:
Get tutor helpright-arrow

Posted 9 months ago

Question
∑n=1∞3nn2n!\sum_{n=1}^{\infty}\frac{3^{n}n^{2}}{n!}
Get tutor helpright-arrow

Posted 8 months ago

Question
f)lim⁡n→+∞[2n+(35)n] f) \lim_{n \to +\infty}\left[\frac{2}{n}+\left(\frac{3}{5}\right)^n\right]
Get tutor helpright-arrow

Posted 8 months ago

Question
∫1cos⁡(x)2 dx\int \frac{1}{\cos(x)^{2}}\,dx
Get tutor helpright-arrow

Posted 8 months ago

View all (198)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant