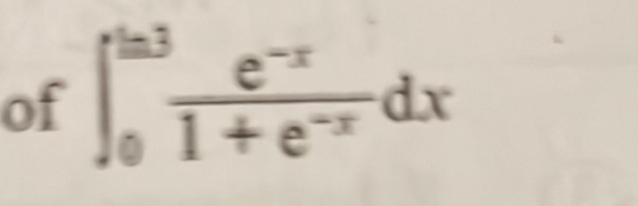AI tutor
Full solution
Q. Evaluate the limit:
- Substitution and Simplification: Simplify the integrand by using a substitution. Let , which implies that . We need to express in terms of .
- Calculate : Calculate from the substitution. implies . Now we can substitute this into the integral.
- Change Limits of Integration: Change the limits of integration according to the substitution.When , .When , .
- Rewrite Integral with New Variable: Rewrite the integral with the new variable and limits.The integral becomes . The negative sign comes from the substitution.
- Evaluate Integral: Evaluate the integral with the new variable.The integral of is . So we have evaluated from to .
- Apply Fundamental Theorem of Calculus: Apply the Fundamental Theorem of Calculus. We need to calculate from to , which is .
- Simplify Result: Simplify the result. .
- Check for Errors: Check for any mathematical errors in the previous steps.No mathematical errors were made in the previous steps.