$\log _{8} 64=$

Full solution

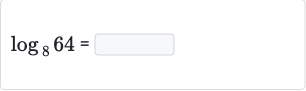
\log _{8} 64=

Problem Statement: We need to find the value of the logarithm of $64$ with base $8$ . The logarithm $\log_{b}a$ answers the question: ＂To what power must the base $b$ be raised, to produce the number $a$ ?＂ In this case, we are looking for the power to which $8$ must be raised to get $64$ .
Understanding Logarithms: We know that $8$ is $2$ raised to the power of $3$ , i.e., $8 = 2^3$ . Similarly, $64$ is $2$ raised to the power of $6$ , i.e., $64 = 2^6$ . We can use these equalities to rewrite the logarithm in terms of base $2$ .
Using Change of Base Formula: Using the change of base formula for logarithms, we can express $\log_{8}64$ as $\log_{2^3}(2^6)$ . This can be simplified by using the property of logarithms that $\log_{b^m}(a^n) = \frac{n}{m} \cdot \log_{b}a$ . Since $a$ is the same as $b$ in this case, $\log_{b}b = 1$ .
Applying Logarithm Property: Applying the property, we get $\log_{2^3}(2^6) = \left(\frac{6}{3}\right) \cdot \log_{2}2$ . Since $\log_{2}2 = 1$ (because $2$ to the power of $1$ is $2$ ), we simplify this to $\left(\frac{6}{3}\right) \cdot 1$ .
Calculating the Final Result: Calculating $(\frac{6}{3}) \times 1$ gives us $2 \times 1$ , which equals $2$ . Therefore, $\log_{8}64 = 2$ .