Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

log_(3)27=

$\log _{3} 27=$

View step-by-step help

View step-by-step help

Relationship between squares and square roots

Full solution

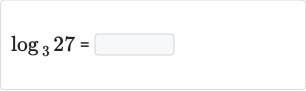
Q.

\log _{3} 27=

Problem Statement: We are asked to find the value of $\log_{3}27$ . The logarithm $\log_{b}a$ answers the question: ＂To what power must the base $b$ be raised, to produce the number $a$ ?＂ In this case, we want to know to what power we must raise $3$ to get $27$ .
Identifying the Power of $3$ : We know that $27$ is a power of $3$ because $3^3 = 27$ . This means that the exponent to which the base $3$ must be raised to get $27$ is $3$ .
Calculating the Logarithm: Therefore, $\log_{3}27$ is equal to $3$ , because $3$ raised to the power of $3$ gives us $27$ .

More problems from Relationship between squares and square roots

Question

Solve the following equation for

y

\newline

\begin{array}{l} y+6=\sqrt{2 y^{2}+72} \\ y=\square \end{array}

Posted 3 months ago

Question

z=12.1+29 i

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 3 months ago

Question

z=-400 i-44.5

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 3 months ago

Question

z=-91+14.6 i

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 3 months ago

Question

z=44 i+23.3

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 3 months ago

Question

\log _{16} 8=

Posted 3 months ago

Question

\log _{5} 25=

Posted 3 months ago

Question

\log _{49} 7=

Posted 3 months ago

Question

\log _{7} 49=

Posted 3 months ago

Question

56x8

Posted 8 hours ago