Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

log_(16)8=

$\log _{16} 8=$

View step-by-step help

View step-by-step help

Relationship between squares and square roots

Full solution

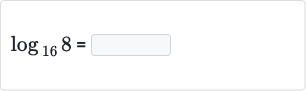
Q.

\log _{16} 8=

Find Logarithm Value: We need to find the value of $\log_{16}8$ . This means we are looking for the exponent that $16$ must be raised to in order to get $8$ .
Express in Powers of $2$ : Since $16$ is $2$ raised to the $4$ th power ( $16 = 2^4$ ), we can express $8$ as a power of $2$ as well, which is $2^3$ (since $8 = 2^3$ ).
Rewrite in Base $2$ : Now we can rewrite the logarithm in terms of base $2$ : $\log_{16}8 = \log_{2^4}(2^3)$ .
Simplify Using Property: Using the property of logarithms that $\log_{b^k}(a^k) = \log_b(a)$ , we can simplify the expression to $\log_{2^4}(2^3) = \left(\frac{3}{4}\right) \cdot \log_{2}(2)$ .
Evaluate Logarithm: Since $\log_{2}(2)$ is $1$ (because $2$ raised to the power of $1$ is $2$ ), we can simplify further: $(\frac{3}{4}) \times \log_{2}(2) = (\frac{3}{4}) \times 1$ .
Final Result: Multiplying $(\frac{3}{4})$ by $1$ gives us $\frac{3}{4}$ . So, $\log_{16}8 = \frac{3}{4}$ .

More problems from Relationship between squares and square roots

Question

Solve the following equation for

y

\newline

\begin{array}{l} y+6=\sqrt{2 y^{2}+72} \\ y=\square \end{array}

Posted 3 months ago

Question

z=12.1+29 i

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 3 months ago

Question

z=-400 i-44.5

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 3 months ago

Question

z=-91+14.6 i

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 3 months ago

Question

z=44 i+23.3

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 3 months ago

Question

\log _{5} 25=

Posted 3 months ago

Question

\log _{49} 7=

Posted 3 months ago

Question

\log _{3} 27=

Posted 3 months ago

Question

\log _{7} 49=

Posted 3 months ago

Question

56x8

Posted 8 hours ago