Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

log_(2)32=

$\log _{2} 32=$

View step-by-step help

View step-by-step help

Relationship between squares and square roots

Full solution

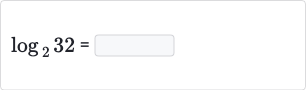
Q.

\log _{2} 32=

Problem statement: We need to find the value of $\log_{2}32$ . This means we are looking for the power to which the base $2$ must be raised to get $32$ .
Equation setup: We know that $2$ raised to some power gives us $32$ . We can write this as $2^x = 32$ . Now we need to find the value of $x$ .
Expressing $32$ as a power of $2$ : We can express $32$ as a power of $2$ . Since $32$ is $2$ multiplied by itself $5$ times, we can write $32$ as $2^5$ .
Equating the exponents: Now we have $2^x = 2^5$ . Since the bases are the same, the exponents must be equal. Therefore, $x$ must be $5$ .
Final result: So, $\log_{2}32$ is equal to $5$ . This is because $2$ raised to the power of $5$ gives us $32$ .

More problems from Relationship between squares and square roots

Question

Solve the following equation for

y

\newline

\begin{array}{l} y+6=\sqrt{2 y^{2}+72} \\ y=\square \end{array}

Posted 3 months ago

Question

z=12.1+29 i

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 3 months ago

Question

z=-400 i-44.5

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 3 months ago

Question

z=-91+14.6 i

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 3 months ago

Question

z=44 i+23.3

\newline

What is the real part of

z

\newline

What is the imaginary part of

z

Posted 3 months ago

Question

\log _{16} 8=

Posted 3 months ago

Question

\log _{5} 25=

Posted 3 months ago

Question

\log _{49} 7=

Posted 3 months ago

Question

\log _{3} 27=

Posted 3 months ago

Question

\log _{7} 49=

Posted 3 months ago