AI tutor
Full solution
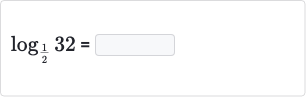
Q.
- Find logarithm of : We need to find the value of the logarithm of with base . This means we are looking for the exponent that we need to raise to in order to get .
- Express as a power of : We can rewrite as a power of , since is raised to the th power: .
- Convert logarithm to base : Now, we can express the logarithm in terms of base : is the same as asking "to what power must we raise to get ?" Since raising a number to a negative exponent is the same as taking the reciprocal of the base raised to the positive exponent, we can write this as .
- Evaluate logarithm of : We know that because the base and the argument are the same, and the exponent is the answer to the logarithm.
- Final result: Therefore, .