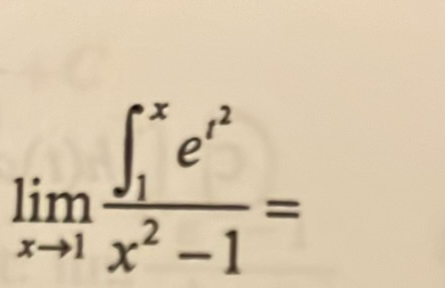lim_(x rarr1)(int_(1)^(x)e^(t^(2)))/(x^(2)-1)=

Question

Bytelearn · Accepted Answer

Recognize Indeterminate Form: Recognize that the limit involves an indeterminate form. As x approaches 1, the numerator approaches the value of the integral from 1 to 1, which is 0 because the limits of integration are the same. The denominator approaches 0 as well because (1^2 - 1) = 0. This creates an indeterminate form of 0/0.Apply L'Hôpital's Rule: Apply L'Hôpital's Rule. Since we have an indeterminate form of 0/0, we can apply L'Hôpital's Rule, which states that if the limit as x approaches a of f(x)/g(x) is 0/0 or ±∞/±∞, then the limit is the same as the limit of the derivatives of the numerator and the denominator, provided that the latter limit exists.Differentiate Numerator: Differentiate the numerator with respect to x. The numerator is an integral with a variable upper limit of integration. The derivative of such an integral with respect to its upper limit is simply the integrand evaluated at the upper limit. Therefore, the derivative of the numerator with respect to x is e^(x^2).Differentiate Denominator: Differentiate the denominator with respect to x. The denominator is x^2 - 1. The derivative of x^2 with respect to x is 2x, and the derivative of -1 is 0. Therefore, the derivative of the denominator with respect to x is 2x.Apply Derivatives to Rule: Apply the derivatives to L'Hôpital's Rule. Now that we have the derivatives, we can apply L'Hôpital's Rule to find the limit: lim_(x -> 1) (e^(x^2)) / (2x)Evaluate Limit of Derivatives: Evaluate the limit of the derivatives. As x approaches 1, e^(x^2) approaches e^(1^2) = e, and 2x approaches 2(1) = 2. Therefore, the limit is e/2.

$\lim _{x \rightarrow 1} \frac{\int_{1}^{x} e^{t^{2}}}{x^{2}-1}=$

Full solution

More problems from Evaluate definite integrals using the chain rule

Related topics

lim⁡x→1∫1xet2x2−1= \lim _{x \rightarrow 1} \frac{\int_{1}^{x} e^{t^{2}}}{x^{2}-1}= limx→1​x2−1∫1x​et2​=

$\lim _{x \rightarrow 1} \frac{\int_{1}^{x} e^{t^{2}}}{x^{2}-1}=$