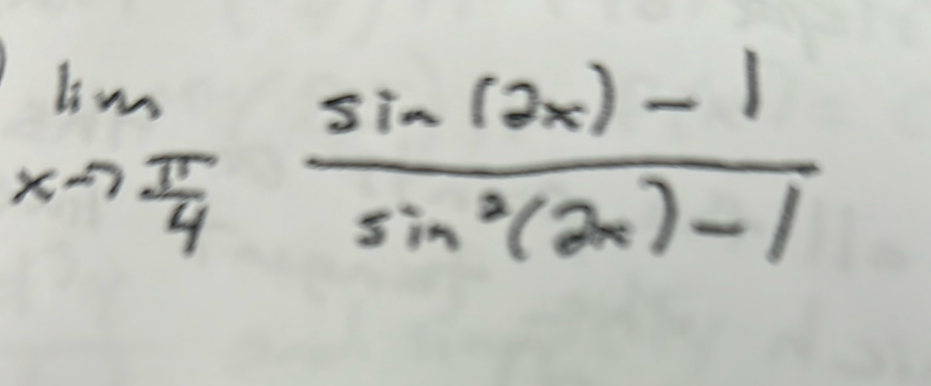AI tutor
Full solution
Q.
- Simplify Expression: We are asked to find the limit of the function as approaches . Let's first simplify the expression if possible before substituting the value of .
- Factorize Difference of Squares: Notice that is a difference of squares which can be factored as .
- Cancel Common Terms: Now we can rewrite the original expression by canceling out the common terms in the numerator and the denominator:
- Substitute x Value: Next, we substitute into the simplified expression:
- Evaluate Limit: Since is equal to , we have:
- Final Result: Therefore, the limit of the function as approaches is .