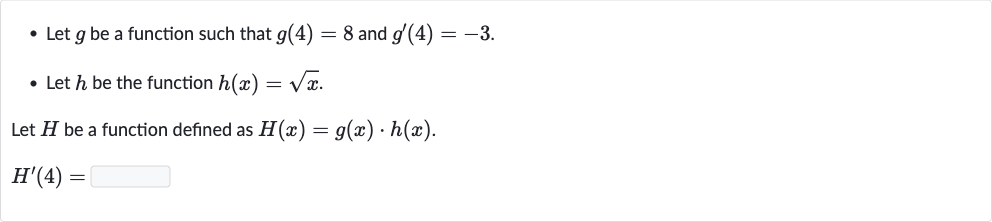Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Let g be a function such that g(4)=8 and g^(')(4)=-3. Let h be the function h(x)=sqrtx. Let H be a function defined as H(x)=g(x)*h(x). H^(')(4)=

- Let g g be a function such that g(4)=8 g(4)=8 and g′(4)=−3 g^{\prime}(4)=-3 .\newline- Let h h be the function h(x)=x h(x)=\sqrt{x} .\newlineLet H H be a function defined as H(x)=g(x)⋅h(x) H(x)=g(x) \cdot h(x) .\newlineH′(4)= H^{\prime}(4)=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Transformations of absolute value functionsright chevron icon

Full solution

Q. - Let g g be a function such that g(4)=8 g(4)=8 and g′(4)=−3 g^{\prime}(4)=-3 .\newline- Let h h be the function h(x)=x h(x)=\sqrt{x} .\newlineLet H H be a function defined as H(x)=g(x)⋅h(x) H(x)=g(x) \cdot h(x) .\newlineH′(4)= H^{\prime}(4)=
  1. Product Rule Derivative: To find H′(4)H'(4), we need to use the product rule for derivatives, which states that (fg)′=f′g+fg′(fg)' = f'g + fg'.
  2. Find h(4)h(4): We know g(4)=8g(4)=8 and g′(4)=−3g'(4)=-3. We need to find h(4)h(4) and h′(4)h'(4).
  3. Calculate h(4)h(4): Calculate h(4)h(4) by substituting xx with 44 in h(x)=xh(x)=\sqrt{x}. So, h(4)=4=2h(4)=\sqrt{4}=2.
  4. Find h′(x)h'(x): To find h′(x)h'(x), we differentiate h(x)=xh(x)=\sqrt{x}. The derivative of x\sqrt{x} is 12x\frac{1}{2\sqrt{x}}.
  5. Calculate h′(4)h'(4): Now calculate h′(4)h'(4) by substituting xx with 44 in h′(x)=12xh'(x)=\frac{1}{2\sqrt{x}}. So, h′(4)=124=14h'(4)=\frac{1}{2\sqrt{4}}=\frac{1}{4}.
  6. Apply Product Rule: Apply the product rule: H′(x)=g′(x)h(x)+g(x)h′(x)H'(x) = g'(x)h(x) + g(x)h'(x).
  7. Substitute Values: Substitute the known values into the product rule to find H′(4)H'(4): H′(4)=g′(4)h(4)+g(4)h′(4)H'(4) = g'(4)h(4) + g(4)h'(4).
  8. Calculate H′(4)H'(4): H′(4)=(−3)(2)+(8)(14)H'(4) = (-3)(2) + (8)(\frac{1}{4}).
  9. Final Calculation: Calculate H′(4)H'(4): H′(4)=−6+2H'(4) = -6 + 2.

More problems from Transformations of absolute value functions

Question
We want to factor the following expression:\newlinex4+9 x^{4}+9 \newlineWhich pattern can we use to factor the expression?\newlineU U and V V are either constant integers or single-variable expressions.\newlineChoose 11 answer:\newline(A) (U+V)2 (U+V)^{2} or (U−V)2 (U-V)^{2} \newline(B) (U+V)(U−V) (U+V)(U-V) \newline(C) We can't use any of the patterns.
Get tutor helpright-arrow

Posted 4 months ago

Question
z=−19+3.14i z=-19+3.14 i \newlineWhat are the real and imaginary parts of z z ?\newlineChoose 11 answer:\newline(A)\newlineRe⁡(z)=−19 and Im⁡(z)=3.14 \begin{array}{l} \operatorname{Re}(z)=-19 \text { and } \\ \operatorname{Im}(z)=3.14 \end{array} \newline(B)\newlineRe⁡(z)=3.14i and Im⁡(z)=−19 \begin{array}{l} \operatorname{Re}(z)=3.14 i \text { and } \\ \operatorname{Im}(z)=-19 \end{array} \newline(c)\newlineRe⁡(z)=−19 and Im⁡(z)=3.14i \begin{array}{l} \operatorname{Re}(z)=-19 \text { and } \\ \operatorname{Im}(z)=3.14 i \end{array} \newline(D)\newlineRe⁡(z)=3.14 and Im⁡(z)=−19 \begin{array}{l} \operatorname{Re}(z)=3.14 \text { and } \\ \operatorname{Im}(z)=-19 \end{array}
Get tutor helpright-arrow

Posted 4 months ago

Question
z=−60−12iRe⁡(z)=Im⁡(z)= \begin{array}{l}z=-60-12 i \\ \operatorname{Re}(z)= \\ \operatorname{Im}(z)=\end{array}
Get tutor helpright-arrow

Posted 4 months ago

Question
z=−45i−15.5 z=-45 i-15.5 \newlineWhat are the real and imaginary parts of z z ?\newlineChoose 11 answer:\newline(A)\newlineRe⁡(z)=−45 and Im⁡(z)=−15.5 \begin{array}{l} \operatorname{Re}(z)=-45 \text { and } \\ \operatorname{Im}(z)=-15.5 \end{array} \newline(B)\newlineRe⁡(z)=−15.5 and Im⁡(z)=−45 \begin{array}{l} \operatorname{Re}(z)=-15.5 \text { and } \\ \operatorname{Im}(z)=-45 \end{array} \newline(C)\newlineRe⁡(z)=−45i and Im⁡(z)=−15.5 \begin{array}{l} \operatorname{Re}(z)=-45 i \text { and } \\ \operatorname{Im}(z)=-15.5 \end{array} \newline(D)\newlineRe⁡(z)=−15.5 and Im⁡(z)=−45i \begin{array}{l} \operatorname{Re}(z)=-15.5 \text { and } \\ \operatorname{Im}(z)=-45 i \end{array}
Get tutor helpright-arrow

Posted 4 months ago

Question
z=−12i+11 z=-12 i+11 \newlineWhat are the real and imaginary parts of z z ?\newlineChoose 11 answer:\newline(A)\newlineRe⁡(z)=11 and Im⁡(z)=−12 \begin{array}{l} \operatorname{Re}(z)=11 \text { and } \\ \operatorname{Im}(z)=-12 \end{array} \newline(B)\newlineRe⁡(z)=11 and Im⁡(z)=−12i \begin{array}{l} \operatorname{Re}(z)=11 \text { and } \\ \operatorname{Im}(z)=-12 i \end{array} \newline(C)\newlineRe⁡(z)=−12i and Im⁡(z)=11 \begin{array}{l} \operatorname{Re}(z)=-12 i \text { and } \\ \operatorname{Im}(z)=11 \end{array} \newline(D)\newlineRe⁡(z)=−12 and Im⁡(z)=11 \begin{array}{l} \operatorname{Re}(z)=-12 \text { and } \\ \operatorname{Im}(z)=11 \end{array}
Get tutor helpright-arrow

Posted 4 months ago

Question
(18+4i)+(−11+23i)= (18+4 i)+(-11+23 i)= \newlineExpress your answer in the form (a+bi) (a+b i) .
Get tutor helpright-arrow

Posted 4 months ago

Question
(14+60i)+(−30+2i)= (14+60 i)+(-30+2 i)= \newlineExpress your answer in the form (a+bi) (a+b i) .
Get tutor helpright-arrow

Posted 4 months ago

Question
(3−91i)+(67)= (3-91 i)+(67)= \newlineExpress your answer in the form (a+bi) (a+b i) .
Get tutor helpright-arrow

Posted 4 months ago

Question
(−71+2i)+(88−12i)= (-71+2 i)+(88-12 i)= \newlineExpress your answer in the form (a+bi) (a+b i) .
Get tutor helpright-arrow

Posted 4 months ago

Question
(−33−2i)−(50+9i)= (-33-2 i)-(50+9 i)= \newlineExpress your answer in the form (a+bi) (a+b i) .
Get tutor helpright-arrow

Posted 4 months ago

View all (6)