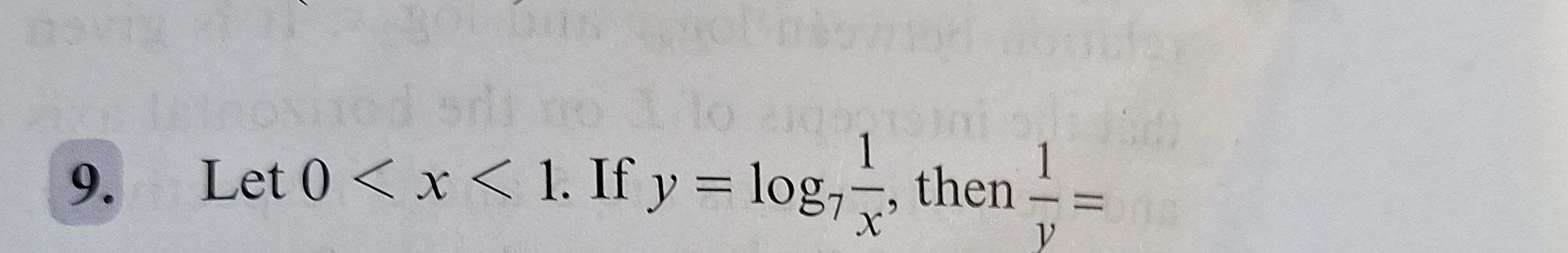Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Let
0 < x < 1. If
y=log_(7)((1)/(x)), then
(1)/(y)=

Let $0<x<1$ . If $y=\log _{7} \frac{1}{x}$ , then $\frac{1}{y}=$

View step-by-step help

View step-by-step help

Intermediate Value Theorem

Full solution

Q. Let

0<x<1

. If

y=\log _{7} \frac{1}{x}

, then

\frac{1}{y}=

Express $y$ in terms of $x$ : Let's start by expressing $y$ in terms of $x$ using the given logarithmic equation $y = \log_7(\frac{1}{x})$ .
Use logarithmic function property: We know that the logarithmic function $\log_b(a) = c$ means that $b^c = a$ . So, in our case, $7^y = \frac{1}{x}.$
Find reciprocal of $7^y$ : Now, we want to find the value of $\frac{1}{y}$ . To do this, we can take the reciprocal of both sides of the equation $7^y = \frac{1}{x}$ to get $7^{-y} = x$ .
Determine $-y$ in terms of $x$ : Since $7^{(-y)}$ is the reciprocal of $7^y$ , and we have $7^{(-y)} = x$ , it follows that $-y$ is the logarithm base $7$ of $x$ , or $-y = \log_7(x)$ .
Calculate $1/y$ : Therefore, $1/y$ is the negative reciprocal of $\log_7(x)$ , which means $1/y = -1/(\log_7(x))$ .
Consider original expression: However, we need to be careful here. The original question asks for $\frac{1}{y}$ in terms of the original expression $y=\log_7(\frac{1}{x})$ . We have found that $\frac{1}{y} = -\frac{1}{\log_7(x)}$ , but we need to express it in terms of the original variable, which is $\frac{1}{x}$ , not $x$ .
Analyze $\log_7(\frac{1}{x})$ : Since $x$ is between $0$ and $1$ , $\frac{1}{x}$ is greater than $1$ . Therefore, $\log_7(\frac{1}{x})$ is negative because $7$ raised to any positive power will be greater than $1$ , and we are taking the log of a number less than $1$ .
Determine sign of $1/y$ : Given that $y = \log_7(1/x)$ and $y$ is negative, $1/y$ is the negative reciprocal of a negative number, which is positive. So, $1/y = -1/(\log_7(1/x))$ .
Express $1/y$ in terms of $y$ : Finally, we can simplify this to $1/y = -1/(-y)$ since $y = \log_7(1/x)$ .
Simplify the expression: Simplifying further, we get $\frac{1}{y} = \frac{1}{y}$ , which means that $\frac{1}{y}$ is simply the reciprocal of $y$ .

More problems from Intermediate Value Theorem

Question

Which of the following functions are continuous for all real numbers?

\newline

g(x)=\ln (x)

\newline

f(x)=\frac{1}{x}

\newline

1

\newline

g

\newline

f

\newline

g

f

\newline

g

f

Posted 3 months ago

Question

\newline

f(x)=\left\{\begin{array}{ll} \ln (-x)+3 & \text { for } x<-3 \\ \ln (-x+3) & \text { for }-3 \leq x<3 \end{array}\right.

\newline

f

x=-3

\newline

1

\newline

\newline

\mathrm{No}

Posted 2 months ago

Question

\newline

f(x)=\left\{\begin{array}{ll}\ln (x) & \text { for } 0<x \leq 2 \\ x^{2} \ln (2) & \text { for } x>2\end{array}\right.

\newline

f

x=2

\newline

1

\newline

\newline

\mathrm{No}

Posted 3 months ago

Question

\newline

g(x)=\left\{\begin{array}{ll} \frac{1}{\cos (x)} & \text { for }-\frac{\pi}{2}<x<0 \\ \cos (x+\pi) & \text { for } x \geq 0 \end{array}\right.

\newline

g

x=0

\newline

1

\newline

\newline

Posted 3 months ago

Question

\newline

h(x)=\left\{\begin{array}{ll} 2^{x-1} & \text { for } x<1 \\ 2^{1-x} & \text { for } x \geq 1 \end{array}\right.

\newline

h

x=1

\newline

1

\newline

\newline

Posted 3 months ago

Question

\newline

g(x)=\left\{\begin{array}{ll} (x-2)^{2} & \text { for } x \leq 2 \\ 2-x^{2} & \text { for } x>2 \end{array}\right.

\newline

g

x=2

\newline

1

\newline

\newline

\mathrm{No}

Posted 3 months ago

Question

\newline

g(x)=\left\{\begin{array}{ll} e^{x} & \text { for } x \leq-1 \\ -e^{-x} & \text { for } x>-1 \end{array}\right.

\newline

g

x=-1

\newline

1

\newline

\newline

Posted 3 months ago

Question

\newline

h(x)=\left\{\begin{array}{ll} e^{2 x} & \text { for } x<0 \\ e^{5 x} & \text { for } x \geq 0 \end{array}\right.

\newline

h

x=0

\newline

1

\newline

\newline

Posted 3 months ago

Question

\newline

h(x)=\left\{\begin{array}{cl}\frac{6}{x+5} & \text { for }-5<x<-3 \\ x^{2}-6 & \text { for } x \geq-3\end{array}\right.

\newline

h

x=-3

\newline

1

\newline

\newline

Posted 3 months ago

Question

\newline

g(x)=\left\{\begin{array}{ll}\sin (x) & \text { for } x<0 \\ x^{2} & \text { for } x \geq 0\end{array}\right.

\newline

g

x=0

\newline

1

\newline

\newline

Posted 3 months ago