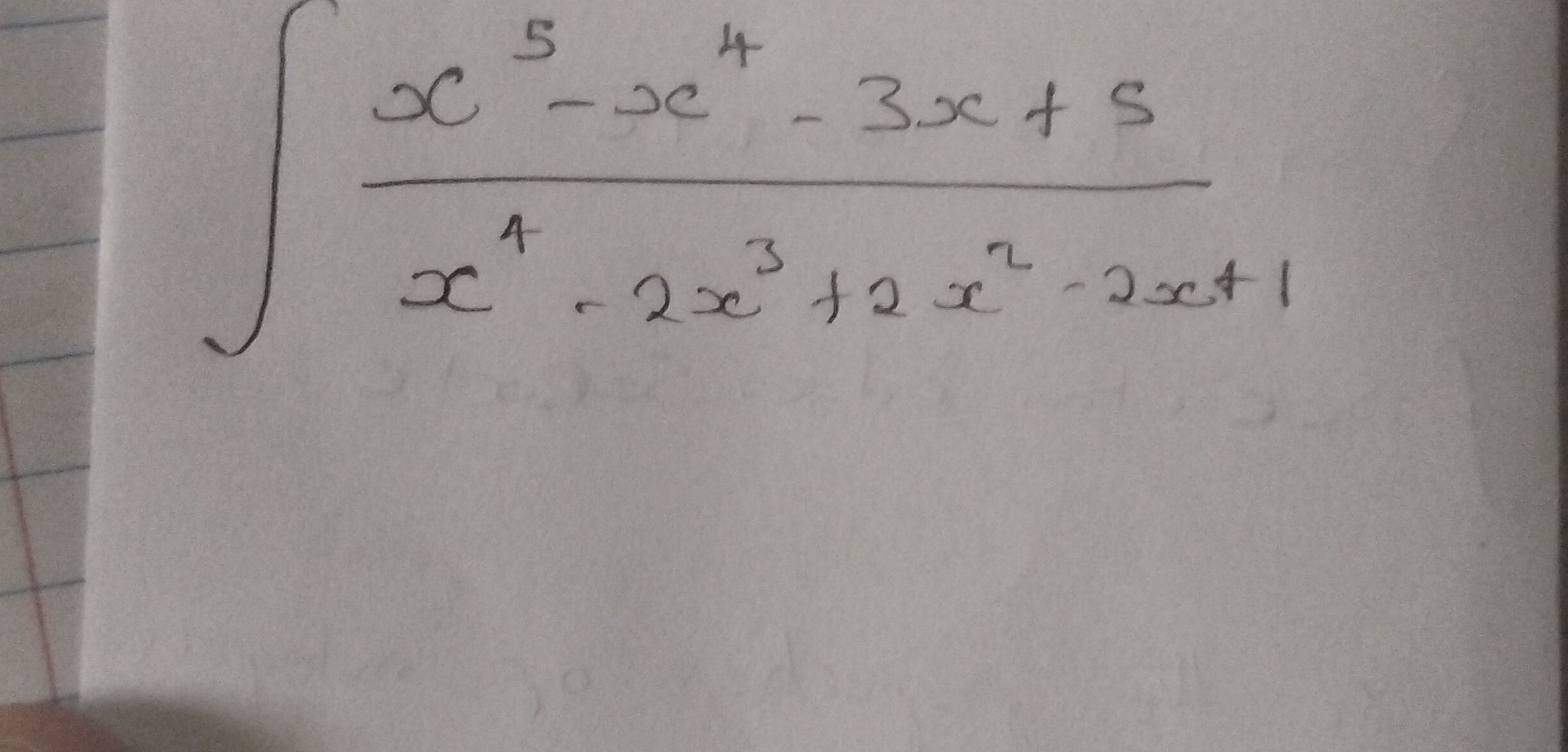AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Evaluate the integral:
Full solution
Q. Evaluate the integral:
- Observe Function: First, we need to observe the function we are integrating. The numerator is a polynomial of degree , and the denominator is a polynomial of degree . We should check if the numerator can be divided by the denominator to simplify the integral.
- Perform Polynomial Division: We perform polynomial long division of the numerator by the denominator. This will allow us to rewrite the integral in a simpler form that may be easier to integrate.
- Consider Partial Fractions: Upon attempting the polynomial long division, we realize that the numerator is of higher degree than the denominator, which means we should be able to divide it at least once. However, the division does not simplify nicely, and we do not get a polynomial plus a remainder that would make the integral straightforward. This suggests that we may need to consider other methods, such as partial fraction decomposition.
- Factor Denominator: Before we can use partial fraction decomposition, we need to factor the denominator if possible. The denominator is a quartic polynomial, which may not factor easily. We should check for any obvious factors or use a factoring algorithm or numerical methods to find the roots.
- Recognize Perfect Square: Upon closer inspection, we notice that the denominator is a perfect square: x^\(2 - x + )^\. This is because x^\(2 - x + )(x^ - x + ) = x^ - x^ + x^ + x^ - x + + x^ - x + = x^ - x^ + x^ - x + \
- Apply Substitution: Now that we know the denominator is a perfect square, we can rewrite the integral as the integral of . However, partial fraction decomposition does not apply here because the numerator is not of lower degree than the denominator squared. We need to consider other methods, such as a substitution or integration by parts.
- Try Integration by Parts: Let's try a substitution. We can let , which means . However, this substitution does not seem to help because the numerator does not match the form we need for , and we would not be able to cancel out all the terms in the numerator.
- Complex Integral Solution: Since substitution does not work, we can try integration by parts. However, integration by parts is typically used when the integral is a product of two functions, and our integral is a quotient. This suggests that integration by parts may not be the right approach either.
- Complex Integral Solution: Since substitution does not work, we can try integration by parts. However, integration by parts is typically used when the integral is a product of two functions, and our integral is a quotient. This suggests that integration by parts may not be the right approach either.We are left with a complex integral that does not simplify easily through standard methods like polynomial long division, partial fraction decomposition, substitution, or integration by parts. This integral may require a more advanced technique or numerical integration for an exact solution. It is also possible that the integral does not have a closed-form solution in terms of elementary functions.
