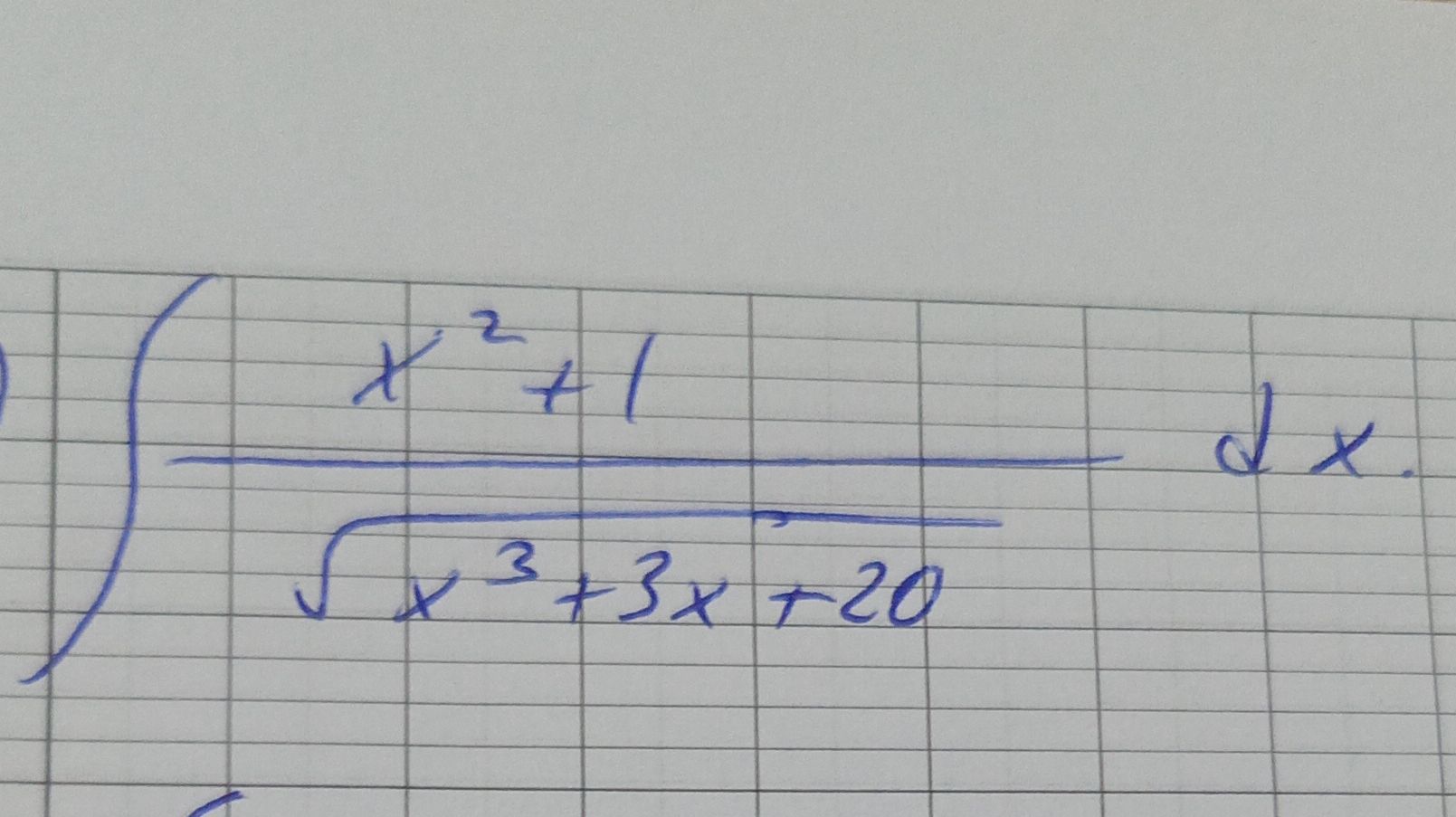AI tutor
Full solution
Q. Evaluate the integral..
- Identify Integral: Identify the integral to be solved.We need to evaluate the integral of the function with respect to .
- Find Substitution: Look for a substitution that simplifies the integral.Let , then . Notice that is part of the derivative of , which suggests that this substitution might be useful.
- Express : Express in terms of and .Since , we can solve for : . We will use this expression to replace in the integral.
- Perform Substitution: Perform the substitution in the integral.Substitute for and for in the integral. The integral becomes:
- Simplify Integral: Simplify the integral.The integral simplifies to:= =
- Integrate with u: Integrate with respect to . The integral of with respect to is , so we have:
- Substitute back: Substitute back for . Replace with to get the final answer: