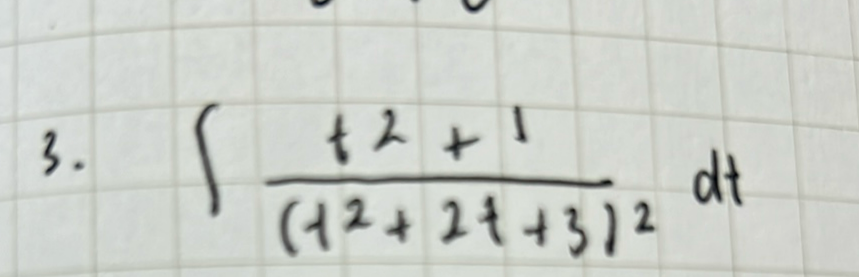
Integrate int(t^(2)+1)/((t^(2)+2t+3)^(2))dt=

Question

Bytelearn · Accepted Answer

Recognize Rational Function: Recognize the integral as a rational function and consider completing the square for the denominator to simplify the integral. The denominator t^2 + 2t + 3 can be written as (t + 1)^2 + 2, which is a completed square plus a constant.Complete Square Denominator: Rewrite the integral with the completed square in the denominator. The integral becomes int (t^2 + 1) / ((t + 1)^2 + 2)^2 dt.Substitution for Simplification: Use substitution to simplify the integral further. Let u = t + 1, which implies du = dt. Then t = u - 1, and we can rewrite t^2 as (u - 1)^2.Rewrite Integral in terms of u: Rewrite the integral in terms of u. The integral becomes int ((u - 1)^2 + 1) / (u^2 + 2)^2 du.Expand and Combine Like Terms: Expand the numerator and combine like terms. The numerator (u - 1)^2 + 1 expands to u^2 - 2u + 1 + 1, which simplifies to u^2 - 2u + 2. The integral is now int (u^2 - 2u + 2) / (u^2 + 2)^2 du.Split Integral into Separate Terms: Split the integral into separate terms. The integral can be split as int u^2 / (u^2 + 2)^2 du - 2 * int u / (u^2 + 2)^2 du + 2 * int 1 / (u^2 + 2)^2 du.Evaluate Each Integral: Evaluate each integral separately. The first integral int u^2 / (u^2 + 2)^2 du can be simplified by noticing that the numerator is the derivative of the denominator. Therefore, we can use the substitution v = u^2 + 2, dv = 2u du, and the integral becomes 1/2 * int 1/v^2 dv, which is -1/2 * 1/v.  The second integral -2 * int u / (u^2 + 2)^2 du is more complex and may require partial fractions or another substitution.  The third integral 2 * int 1 / (u^2 + 2)^2 du can be evaluated using a trigonometric substitution or recognizing it as a standard integral.Identify Mistake: Realize a mistake has been made in the previous step. The first integral was incorrectly simplified. The numerator u^2 is not the derivative of the denominator (u^2 + 2)^2. This is a math error.

Integrate $\int \frac{t^{2}+1}{\left(t^{2}+2 t+3\right)^{2}} d t$ =

Full solution

More problems from Evaluate definite integrals using the chain rule

Related topics

Integrate ∫t2+1(t2+2t+3)2dt \int \frac{t^{2}+1}{\left(t^{2}+2 t+3\right)^{2}} d t ∫(t2+2t+3)2t2+1​dt=

Integrate $\int \frac{t^{2}+1}{\left(t^{2}+2 t+3\right)^{2}} d t$ =