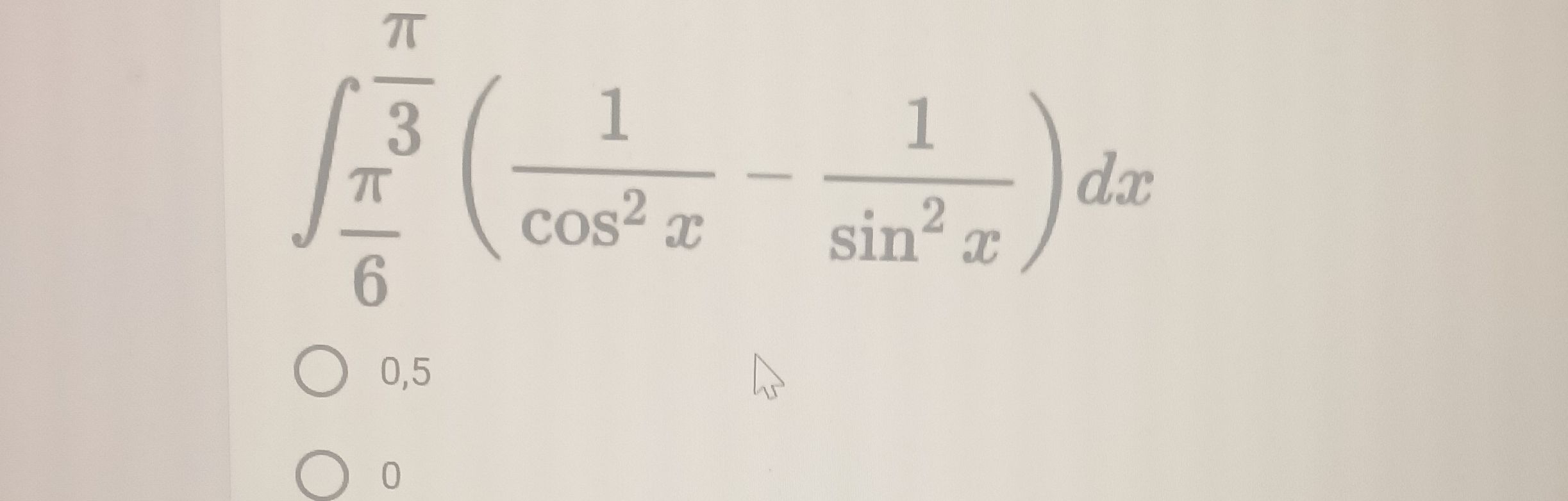AI tutor
Full solution
Q. ,
- Simplify integrand: Step : Simplify the integrand.We start by recognizing that is and is . So, the integral becomes:
- Separate the integral: Step : Separate the integral.The integral of is , and the integral of is . Therefore:
- Evaluate limits: Step : Evaluate from to .Plug in the limits of integration: evaluated from to =
- Calculate values: Step : Calculate the values., , , So,