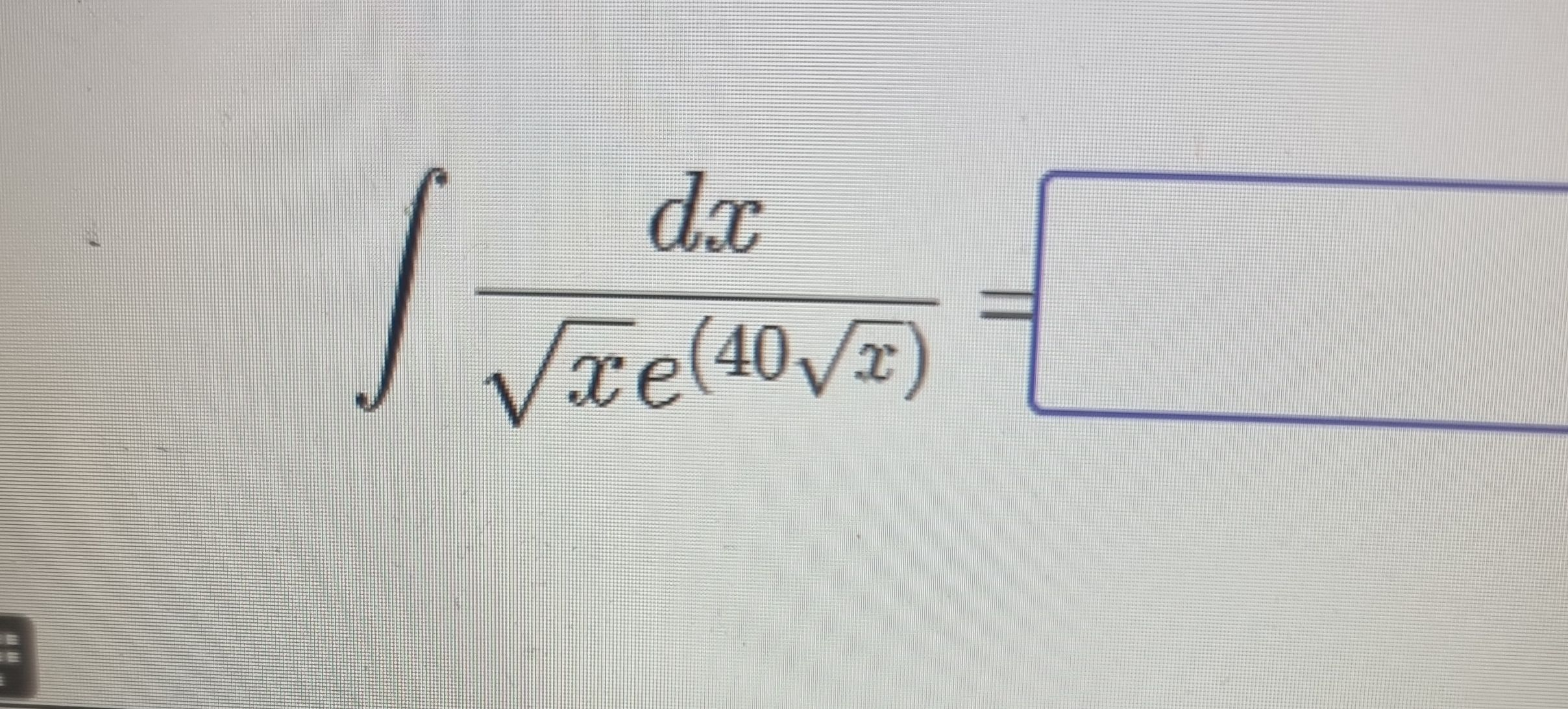AI tutor
Full solution
Q.
- Make Substitution: Simplify the integral by making a substitution.Let , which implies that . Now, differentiate both sides with respect to to find in terms of .
- Rewrite in Terms of : Rewrite the integral in terms of . The integral becomes: Simplify the integrand by canceling in the numerator and denominator.
- Evaluate Integral: Evaluate the integral.The integral of with respect to is a standard exponential integral.
- Substitute Back: Substitute back the original variable .Since , we have:
- Write Final Answer: Write the final answer.The integral of is: