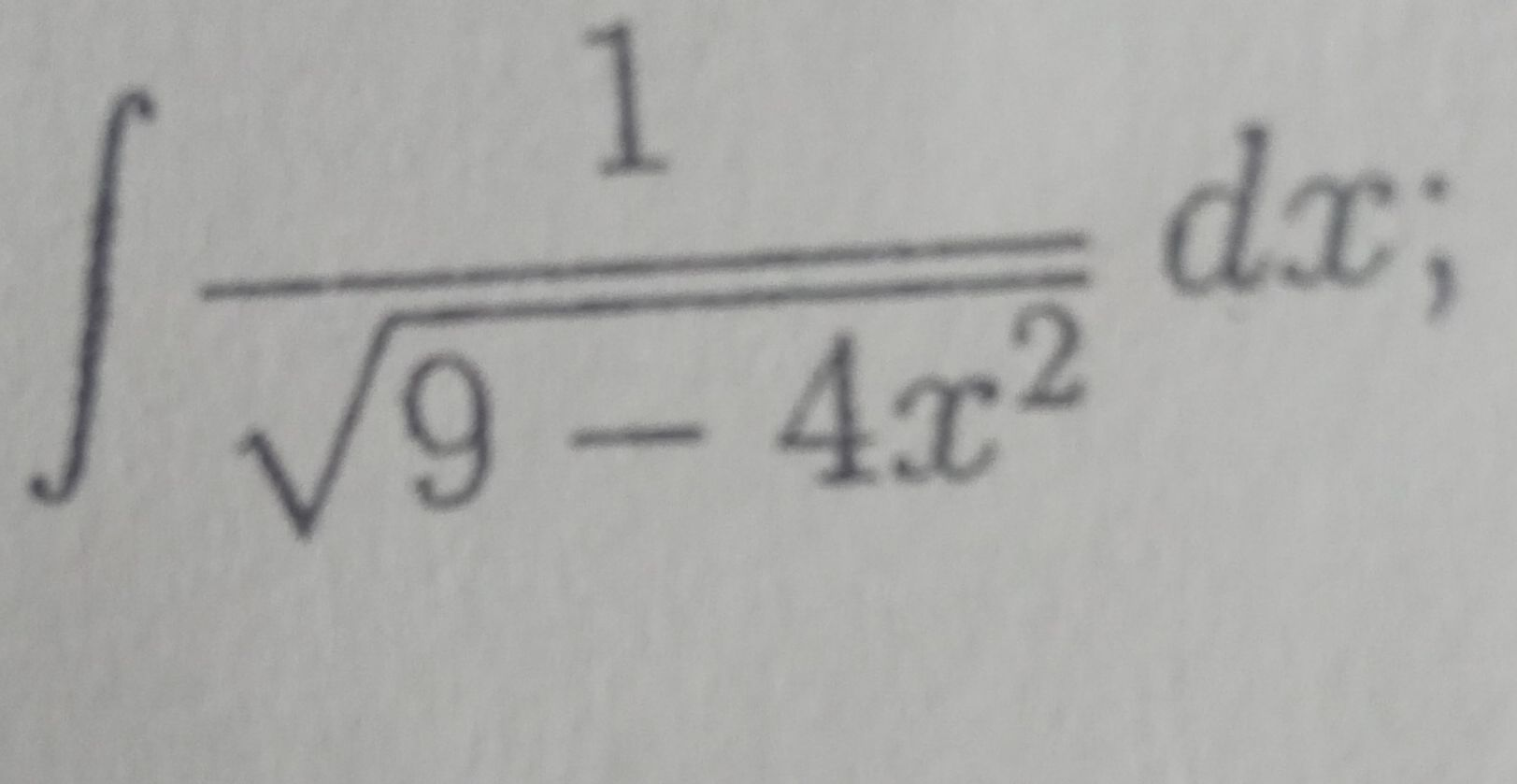AI tutor
Full solution
Q.
- Recognize standard form: Recognize the integral as a standard form. The integral resembles the integral of the form , which is a standard form for the inverse trigonometric function .
- Identify : Identify from the integral.In our integral, , so . This means we can rewrite the integral in terms of a standard function.
- Use substitution : Rewrite the integral using the substitution . Let , then . We need to find the limits of integration in terms of , but since this is an indefinite integral, we will just perform the substitution.
- Substitute and : Substitute and in the integral.Substituting and into the integral, we get .
- Simplify expression: Simplify the integral.Simplify the expression under the square root: .The integral becomes .
- Further simplify integral: Further simplify the integral.Since , the integral simplifies to .
- Integrate with respect to : Integrate with respect to . The integral of with respect to is .
- Substitute back for u: Substitute back for u.We need to express our answer in terms of , so we substitute back using the original substitution . We solve for : , so .
- Write final answer: Write the final answer.The final answer is .