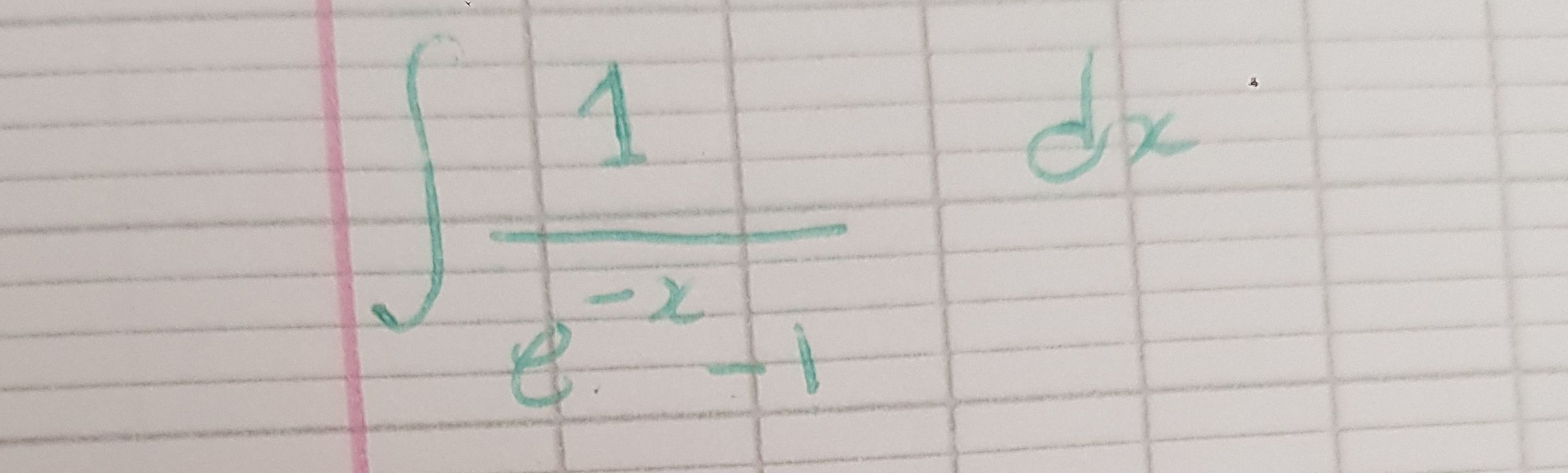Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

int(1)/(e^(-x)-1)dx

$\int \frac{1}{e^{-x}-1} d x$

View step-by-step help

View step-by-step help

Evaluate definite integrals using the chain rule

Full solution

Q.

\int \frac{1}{e^{-x}-1} d x

Simplify integrand: Step $1$ : Simplify the integrand. $\newline$ Rewrite the integrand using the property of exponents: $e^{-x} = 1/e^x$ . $\newline$ So, $1/(e^{-x} - 1)$ becomes $1/(1/e^x - 1)$ . $\newline$ Simplify further: $1/(1/e^x - 1) = e^x/(1 - e^x)$ .
Substitute and simplify: Step $2$ : Substitute to simplify the integral. $\newline$ Let $u = 1 - e^x$ , then $du = -e^x dx$ . $\newline$ Rearrange for $dx$ : $dx = -\frac{du}{e^x}$ . $\newline$ Substitute into the integral: $\int \frac{e^x}{1 - e^x} dx = \int -\frac{du}{u}$ .
Integrate with new variable: Step $3$ : Integrate using the new variable. $\newline$ The integral $\int -\frac{du}{u}$ is $-\ln|u| + C$ .
Substitute back to x: Step $4$ : Substitute back to $x$ . $\newline$ Since $u = 1 - e^x$ , the integral becomes $-\ln|1 - e^x| + C$ .

More problems from Evaluate definite integrals using the chain rule

Question

Consider the following problem:

\newline

The water level under a bridge is changing at a rate of

r(t)=40 \sin \left(\frac{\pi t}{6}\right)

centimeters per hour (where

t

is the time in hours). At time

t=3

, the water level is

91

centimeters. By how much does the water level change during the

4^{\text {th }}

\newline

Which expression can we use to solve the problem?

\newline

1

\newline

\int_{3}^{4} r(t) d t

\newline

\int_{0}^{4} r(t) d t

\newline

\int_{4}^{5} r(t) d t

\newline

\int_{4}^{4} r(t) d t

Posted 2 months ago

Question

s(t)

gives the number of students enrolled in a school by time

t

\newline

\int_{15}^{18} s^{\prime}(t) d t=20

\newline

1

\newline

(A) The rate of change of enrollment is

20

students per year more in year

18

than it was in year

15

\newline

20

more students enrolled in year

18

15

\newline

(C) Between years

15

18

, the cumulative number of years of schooling of all of the enrolled students is

20

\newline

20

students enrolled in year

18

Posted 1 month ago

Question

A water tank is filled at a rate of

r(t)

liters per minute (where

t

is the time in minutes).

\newline

\int_{1}^{7} r^{\prime}(t) d t

\newline

1

\newline

(A) The rate at which the tank was filled at

t=7

\newline

B) The average rate of filling between

t=1

t=7

\newline

(C) The change in the rate of filling between

t=1

t=7

\newline

(D) The amount of water filled between

t=1

t=7

Posted 2 months ago

Question

The base of a solid is the region enclosed by the graphs of

y=\sin (x)

y=4-\sqrt{x}

x=2

x=7

\newline

Cross sections of the solid perpendicular to the

x

-axis are rectangles whose height is

2 x

\newline

Which one of the definite integrals gives the volume of the solid?

\newline

1

\newline

\int_{2}^{7}\left[(4-\sqrt{x})^{2}-\sin ^{2}(x)\right] d x

\newline

\int_{2}^{7}[\sin (x)+\sqrt{x}-4] \cdot 2 x d x

\newline

\int_{2}^{7}\left[\sin ^{2}(x)-(4-\sqrt{x})^{2}\right] d x

\newline

\int_{2}^{7}[4-\sqrt{x}-\sin (x)] \cdot 2 x d x

Posted 1 month ago

Question

Evaluate the integral.

\newline

\int-2 x^{3} \cos (3 x) d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-4 x^{2} 3^{3 x} d x

\newline

Posted 2 months ago

Question

Evaluate the integral.

\newline

\int-4 x^{2} e^{4 x} d x

\newline

Posted 2 months ago

Question

\sum_{n=1}^{\infty}\frac{3^{n}n^{2}}{n!}

Posted 2 months ago

Question

f) \lim_{n \to +\infty}\left[\frac{2}{n}+\left(\frac{3}{5}\right)^n\right]

Posted 2 months ago

Question

\int \frac{1}{\cos(x)^{2}}\,dx

Posted 2 months ago