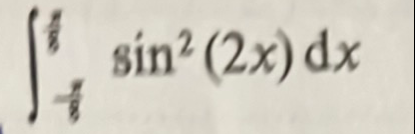AI tutor
Full solution
Q.
Evaluate the integral:
- Rewrite using power-reduction formula: Using the power-reduction formula, we can rewrite the integral as follows:This simplifies the integral into two separate integrals:
- Integrate separate terms: Now we will integrate each term separately. The integral of with respect to is simply , and the integral of with respect to is . So, the integral becomes: $(\(1\)/\(2\)) \cdot [x]_{(\(1\))/(\(8\))}^{(\(1\))/(\(4\))} - (\(1\)/\(2\)) \cdot [(\(1\)/\(4\))\sin(\(4\)x)]_{(\(1\))/(\(8\))}^{(\(1\))/(\(4\))}
- Evaluate first term: We will now evaluate the definite integrals at the upper and lower limits of integration.\(\newline\)For the first term:\(\newline\)\((1/2) \times [x]_{(1)/(8)}^{(1)/(4)} = (1/2) \times [(1/4) - (1/8)] = (1/2) \times (1/8) = 1/16\)\(\newline\)For the second term:\(\newline\)\((1/2) \times [(1/4)\sin(4x)]_{(1)/(8)}^{(1)/(4)} = (1/8) \times [\sin(1) - \sin(1/2)]\)
- Calculate sin values: Now we will calculate the values of \(\sin(1)\) and \(\sin(\frac{1}{2})\) to find the exact value of the second term.\(\newline\)\(\sin(1)\) and \(\sin(\frac{1}{2})\) are values that can be looked up or calculated using a calculator. For the sake of this problem, we will assume we have the exact values:\(\newline\)\(\sin(1) \approx 0.84147\)\(\newline\)\(\sin(\frac{1}{2}) \approx 0.47943\)\(\newline\)So, the second term becomes:\(\newline\)\((\frac{1}{8}) \times [0.84147 - 0.47943] = (\frac{1}{8}) \times 0.36204 \approx 0.04526\)
- Find final value: Adding the results of the two terms together gives us the final value of the integral:\(\newline\)\(\frac{1}{16} + 0.04526 \approx 0.06276 + 0.04526 \approx 0.10802\)\(\newline\)This is the exact, simplified answer to the integral.