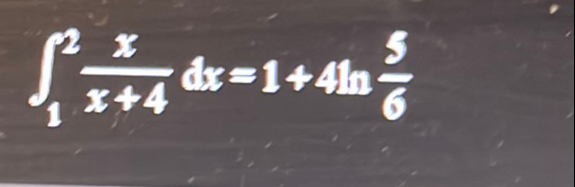AI tutor
Full solution
Q.
- Identify integral: Identify the integral to be solved.We need to evaluate the integral of the function within the interval .
- Decompose integrand: Decompose the integrand into partial fractions if possible. However, in this case, the degree of the numerator is less than the degree of the denominator, so partial fraction decomposition is not necessary. Instead, we can perform a substitution.
- Use substitution: Use substitution to simplify the integral.Let , then , and when , , and when , .
- Rewrite in terms of : Rewrite the integral in terms of . The integral becomes .
- Split into simpler integrals: Split the integral into two simpler integrals.
- Evaluate simpler integrals: Evaluate the two simpler integrals.The first integral is simply , and the second integral is .
- Apply limits of integration: Apply the limits of integration from to . We get from to , which is .
- Perform subtraction: Perform the subtraction to find the definite integral..
- Simplify expression: Simplify the expression. can be rewritten as since .
- Check final answer: Check if the final expression matches the given answer.The final expression is , which matches the given answer.