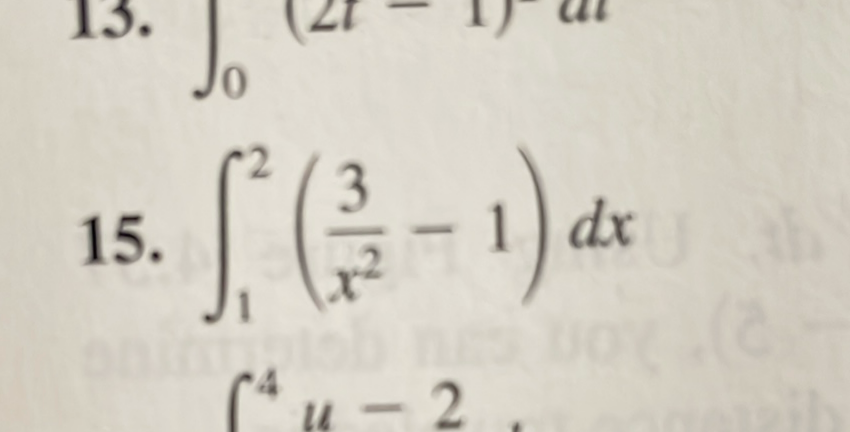AI tutor
Full solution
Q. .
- Identify integral: Identify the integral to be solved.We need to evaluate the integral of the function with respect to from to .
- Break into two integrals: Break the integral into two separate integrals.The integral of a sum or difference of functions is the sum or difference of their integrals. Therefore, we can write:
- Evaluate first integral: Evaluate the first integral . The integral of with respect to is . This is because the integral of is for , and in this case, . So,
- Evaluate second integral: Evaluate the second integral . The integral of with respect to is , because the derivative of with respect to is . So,
- Combine results: Combine the results of Step and Step .The combined integral from to of is: from to
- Evaluate definite integral: Evaluate the definite integral from to . We substitute the upper limit of integration () and then the lower limit () into the antiderivative and subtract the two results: