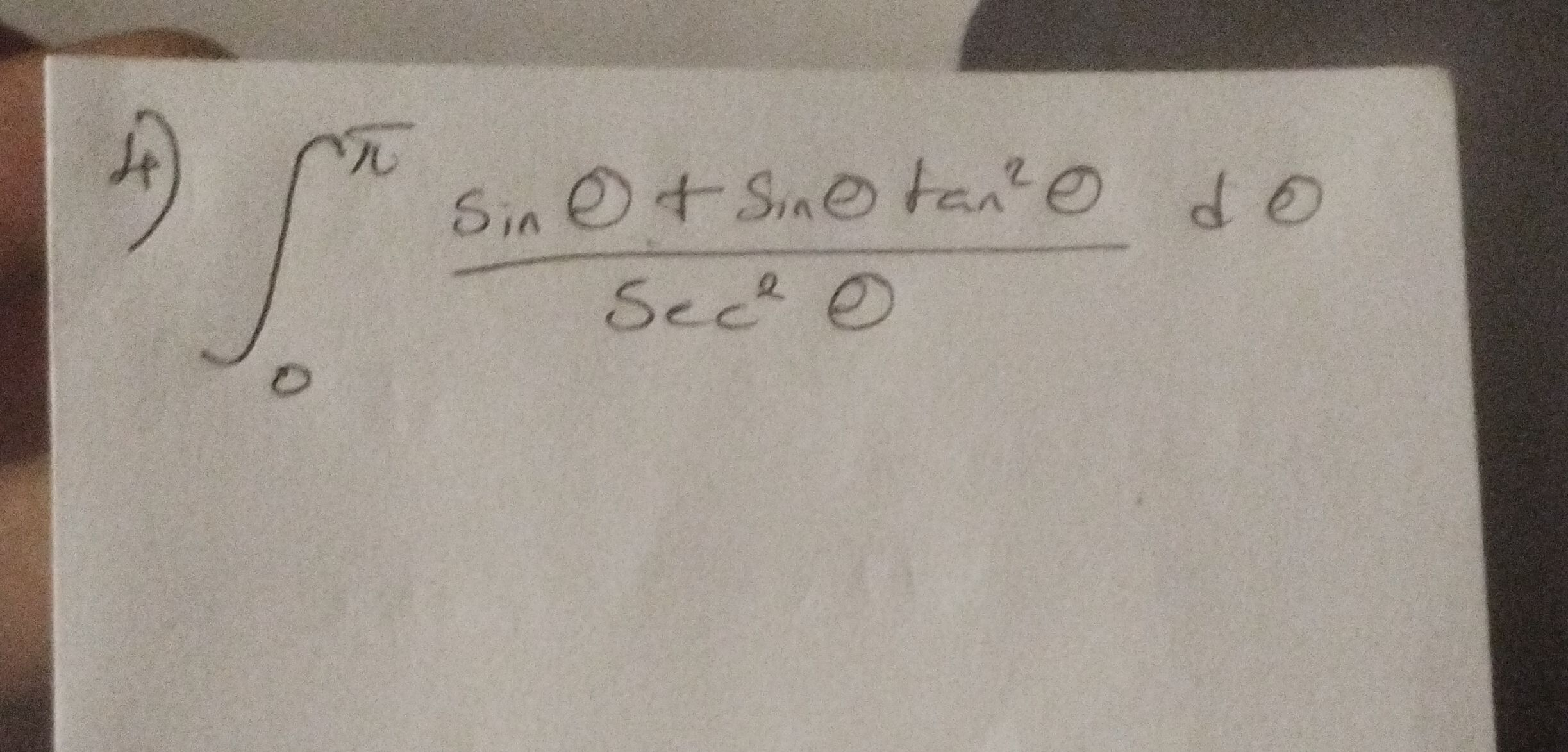int_(0)^(pi)(sin theta+sin thetatan^(2)theta)/(sec^(2)theta)d theta

Question

Bytelearn · Accepted Answer

Trig Identities Simplification: We are given the integral: int_(0)^(pi)(sin(θ) + sin(θ)tan^2(θ))/(sec^2(θ)) dθ First, we simplify the integrand using trigonometric identities. We know that sec(θ) = 1/cos(θ) and tan(θ) = sin(θ)/cos(θ). Therefore, tan^2(θ) = sin^2(θ)/cos^2(θ) and sec^2(θ) = 1/cos^2(θ).Integrand Simplification: We can rewrite the integrand by replacing sec^2(θ) with 1/cos^2(θ) and tan^2(θ) with sin^2(θ)/cos^2(θ): (sin(θ) + sin(θ) * (sin^2(θ)/cos^2(θ))) / (1/cos^2(θ)) This simplifies to: sin(θ)cos^2(θ) + sin^3(θ)Splitting Integrals: Now we can split the integral into two separate integrals: int_(0)^(pi)sin(θ)cos^2(θ) dθ + int_(0)^(pi)sin^3(θ) dθPower-Reducing Formula: Let's first evaluate the integral int_(0)^(pi)sin(θ)cos^2(θ) dθ. We can use the power-reducing formula for cos^2(θ), which is cos^2(θ) = (1 + cos(2θ))/2. The integral becomes: int_(0)^(pi)sin(θ)(1 + cos(2θ))/2 dθEvaluation of First Integral: This integral can be split into two parts: 1/2 int_(0)^(pi)sin(θ) dθ + 1/2 int_(0)^(pi)sin(θ)cos(2θ) dθ The first integral evaluates to 0 because sin(θ) is symmetric about π/2, and the second integral can be solved using the substitution method or by recognizing it as a product of sine and cosine, which also evaluates to 0 due to the periodicity and symmetry of the functions involved.Rewriting Sin^3(θ): Now let's evaluate the integral int_(0)^(pi)sin^3(θ) dθ. We can use the identity sin^2(θ) = 1 - cos^2(θ) to rewrite sin^3(θ) as sin(θ)(1 - cos^2(θ)). The integral becomes: int_(0)^(pi)sin(θ)(1 - cos^2(θ)) dθEvaluation of Second Integral: This integral can be split into two parts: int_(0)^(pi)sin(θ) dθ - int_(0)^(pi)sin(θ)cos^2(θ) dθ As we have already established, both of these integrals evaluate to 0 due to the symmetry of the sine function and the periodicity of the sine and cosine functions.Final Answer: Since both integrals from the previous steps evaluate to 0, the original integral also evaluates to 0. Therefore, the final answer is 0.

$\int_{0}^{\pi} \frac{\sin \theta+\sin \theta \tan ^{2} \theta}{\sec ^{2} \theta} d \theta$

Full solution

More problems from Evaluate definite integrals using the chain rule

Related topics

∫0πsin⁡θ+sin⁡θtan⁡2θsec⁡2θdθ \int_{0}^{\pi} \frac{\sin \theta+\sin \theta \tan ^{2} \theta}{\sec ^{2} \theta} d \theta ∫0π​sec2θsinθ+sinθtan2θ​dθ

$\int_{0}^{\pi} \frac{\sin \theta+\sin \theta \tan ^{2} \theta}{\sec ^{2} \theta} d \theta$