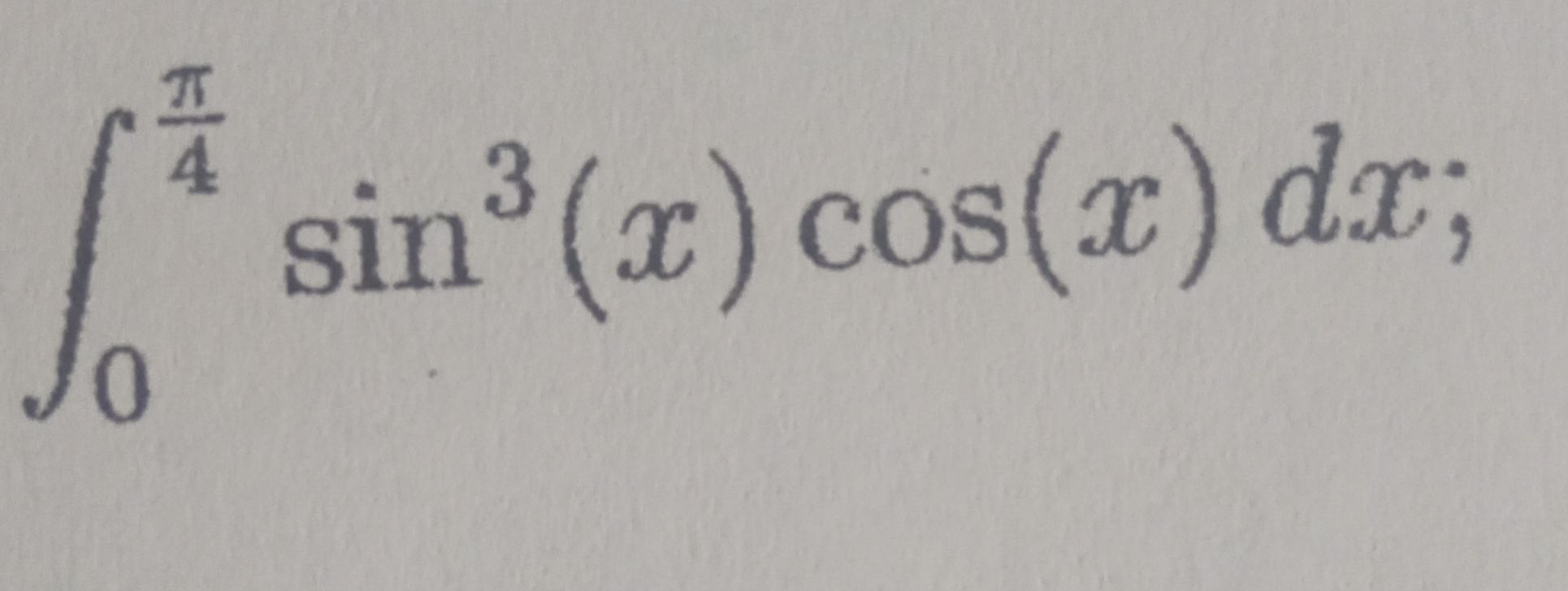AI tutor
Full solution
Q.
- Given Integral: We are given the integral to evaluate: To solve this integral, we can use the power-reducing formula for or we can use a substitution method. Since we have a term and a term, it's convenient to use substitution. Let's let , which means .
- Substitution Method: Now we need to change the limits of integration to match our substitution. When , . When , . So our new limits of integration are from to .
- Limits of Integration: Substituting for and for , we get: ext{int}_{0}^{ rac{ ext{sqrt}(2)}{2}}u^3duThis is a simple power integral that we can evaluate using the power rule for integrals.
- Power Rule Integration: Using the power rule for integrals, we integrate with respect to :
- Apply Limits: Now we apply the limits of integration to the antiderivative:
- Calculate Value: Calculating the value of the antiderivative at the limits, we get:/ = /^ = \frac{^}{^} = \frac{}{}\)And since / = , we don't need to subtract anything.
- Final Result: So the value of the integral is: