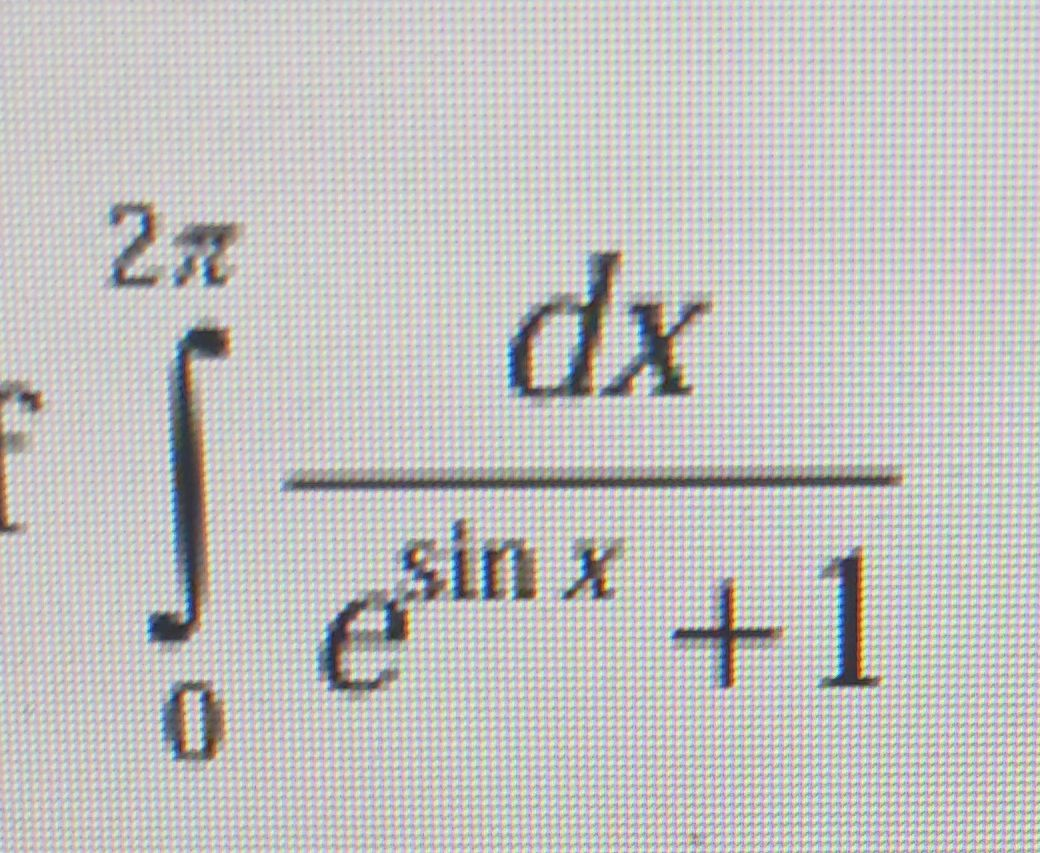AI tutor
Full solution
Q.
- Identify Integral: Identify the integral to be solved.We need to evaluate the integral .
- Recognize Limitation: Recognize that the integral does not have an elementary antiderivative. The function does not have a standard antiderivative, so we cannot apply basic integration techniques directly.
- Consider Symmetry: Consider symmetry or periodic properties of the integrand. Since is a periodic function with a period of , we can consider if the integrand has any symmetry over the interval that could simplify the integral. However, the presence of the exponential function complicates this approach.
- Find Substitution: Look for a substitution or a special technique. In this case, there is no obvious substitution that simplifies the integral, and special techniques like integration by parts or partial fractions do not apply.
- Explore Special Techniques: Consider numerical methods or special functions. Since the integral does not have an elementary antiderivative, we may need to resort to numerical methods to evaluate it or express the solution in terms of special functions.
- Use Numerical Methods: Evaluate the integral using numerical methods.We can use numerical integration techniques such as Simpson's rule, trapezoidal rule, or numerical integration software to approximate the value of the integral.