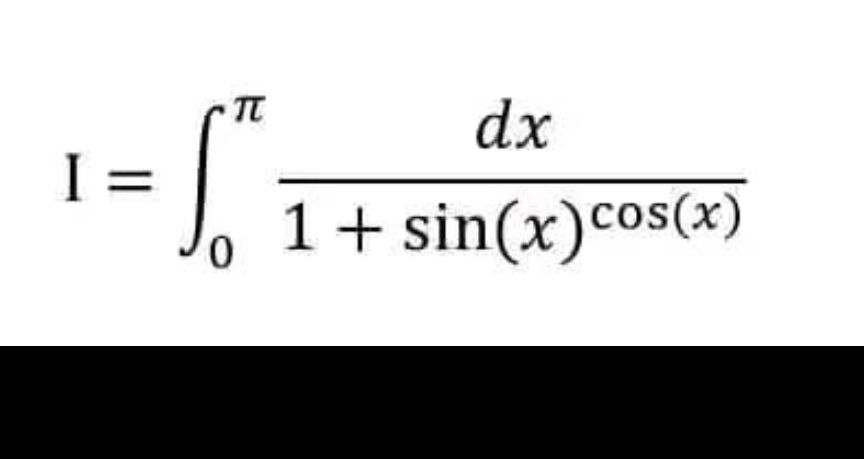I=int_(0)^(pi)(dx)/(1+sin(x)^(cos(x)))

Question

Bytelearn · Accepted Answer

Analyze Integral: Analyze the integral to determine if there are any standard integration techniques that can be applied. The integral I = ∫(dx)/(1+sin(x)^(cos(x))) from 0 to pi does not match any standard integral form, and it is not immediately clear how to simplify the integrand. Therefore, we need to consider alternative methods or substitutions that might simplify the integral.Find Symmetry: Look for symmetry or periodic properties in the integrand that might simplify the integral. The function sin(x) is periodic with a period of 2π, and cos(x) is periodic with a period of 2π as well. However, the combination sin(x)^(cos(x)) does not exhibit a simple periodicity or symmetry that can be exploited over the interval [0, π]. Therefore, we cannot simplify the integral using symmetry arguments.Consider Substitution: Consider a substitution that might simplify the integrand. The integrand is complex due to the presence of sin(x) raised to the power of cos(x). A common substitution for integrals involving trigonometric functions is to use a half-angle or Weierstrass substitution, but in this case, such substitutions do not seem to simplify the integrand. Therefore, we do not have a clear substitution to apply.Evaluate Numerically: Evaluate the integral numerically or conclude that it cannot be expressed in terms of elementary functions. Given the complexity of the integrand and the lack of a clear substitution or simplification, it is likely that this integral cannot be expressed in terms of elementary functions. In such cases, numerical methods or special functions are typically used to evaluate the integral. For the purposes of this problem, we will conclude that the integral cannot be evaluated using standard calculus techniques and must be approached numerically or left unevaluated.Conclude Evaluation: Conclude the evaluation of the integral. Since the integral cannot be evaluated using standard techniques, we conclude that the integral I = ∫(dx)/(1+sin(x)^(cos(x))) from 0 to pi does not have a closed-form expression in terms of elementary functions. The value of the integral would need to be approximated using numerical methods.

$I=\int_{0}^{\pi} \frac{d x}{1+\sin (x)^{\cos (x)}}$

Full solution

More problems from Evaluate definite integrals using the chain rule

Related topics

I=∫0πdx1+sin⁡(x)cos⁡(x) I=\int_{0}^{\pi} \frac{d x}{1+\sin (x)^{\cos (x)}} I=∫0π​1+sin(x)cos(x)dx​

$I=\int_{0}^{\pi} \frac{d x}{1+\sin (x)^{\cos (x)}}$