Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

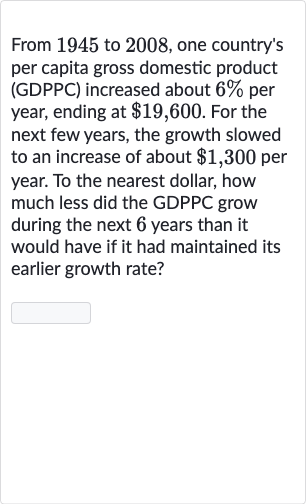
From 1945 to 2008 , one country's per capita gross domestic product (GDPPC) increased about 6% per year, ending at $19,600. For the next few years, the growth slowed to an increase of about $1,300 per year. To the nearest dollar, how much less did the GDPPC grow during the next 6 years than it would have if it had maintained its earlier growth rate? ◻

From 19451945 to 20082008, one country's per capita gross domestic product (GDPPC) increased about 6%6\% per year, ending at $19,600\$19,600. For the next few years, the growth slowed to an increase of about $1,300\$1,300 per year. To the nearest dollar, how much less did the GDPPC grow during the next 66 years than it would have if it had maintained its earlier growth rate?\newline□\square

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 8right chevron icon
Percent of change: word problemsright chevron icon

Full solution

Q. From 19451945 to 20082008, one country's per capita gross domestic product (GDPPC) increased about 6%6\% per year, ending at $19,600\$19,600. For the next few years, the growth slowed to an increase of about $1,300\$1,300 per year. To the nearest dollar, how much less did the GDPPC grow during the next 66 years than it would have if it had maintained its earlier growth rate?\newline□\square
  1. Calculate GDPPC Growth: First, we need to calculate the GDPPC growth over the next 66 years if it had maintained the 6%6\% per year growth rate.\newlineThe formula for compound growth is:\newlineGDPPCend=GDPPCstart×(1+growth_rate)number_of_yearsGDPPC_{\text{end}} = GDPPC_{\text{start}} \times (1 + \text{growth\_rate})^{\text{number\_of\_years}}\newlineHere, GDPPCstartGDPPC_{\text{start}} is $19,600\$19,600, growth_rate\text{growth\_rate} is 6%6\% or 0.060.06, and number_of_years\text{number\_of\_years} is 66.
  2. Perform Calculation: Now, we perform the calculation:\newlineGDPPCend=$(19,600)×(1+0.06)6GDPPC_{\text{end}} = \$(19,600) \times (1 + 0.06)^6\newlineUsing a calculator, we find:\newlineGDPPCend≈$(19,600)×(1.418519)GDPPC_{\text{end}} \approx \$(19,600) \times (1.418519)\newlineGDPPCend≈$(27,803.17)GDPPC_{\text{end}} \approx \$(27,803.17)\newlineThis is the GDPPC at the end of 66 years with a 6%6\% growth rate per year.
  3. Calculate Slower Growth: Next, we calculate the GDPPC growth with the slower rate of $1,300\$1,300 per year for 66 years.\newlineThe formula for linear growth is:\newlineGDPPCend=GDPPCstart+(increase_per_year×number_of_years)\text{GDPPC}_{\text{end}} = \text{GDPPC}_{\text{start}} + (\text{increase\_per\_year} \times \text{number\_of\_years})\newlineHere, GDPPCstart\text{GDPPC}_{\text{start}} is $19,600\$19,600, increase_per_year\text{increase\_per\_year} is $1,300\$1,300, and number_of_years\text{number\_of\_years} is 66.
  4. Find Difference: Now, we perform the calculation:\newlineGDPPCend_{\text{end}} = $19,600\$19,600 + $1,300×6\$1,300 \times 6\newlineGDPPCend_{\text{end}} = $19,600\$19,600 + $7,800\$7,800\newlineGDPPCend_{\text{end}} = $27,400\$27,400\newlineThis is the GDPPC at the end of 66 years with a growth of $1,300\$1,300 per year.
  5. Perform Subtraction: Finally, we find the difference between the GDPPC growth at the 6%6\% rate and the slower $1,300\$1,300 per year rate.\newlineDifference = GDPPC\_end (6%(6\% growth) - GDPPC\_end ($1,300/year(\$1,300/year growth)\newlineDifference = $27,803.17\$27,803.17 - $27,400\$27,400
  6. Perform Subtraction: Finally, we find the difference between the GDPPC growth at the 66\% rate and the slower (\$)\(1\),\(300\) per year rate.\(\newline\)Difference = GDPPC\_end (\(6\)\% growth) - GDPPC\_end (\(\$\)\(1\),\(300\)/year growth)\(\newline\)Difference = \(\$27,803.17 - \$27,400\)Now, we perform the subtraction:\(\newline\)Difference \(\approx \$403.17\)\(\newline\)To the nearest dollar, the GDPPC grew \(\$403\) less during the next \(6\) years than it would have if it had maintained its earlier growth rate of \(6\)\% per year.

More problems from Percent of change: word problems

Question
What is 70%70\% of $10?\$10? \newline $\$ _____
Get tutor helpright-arrow

Posted 2 months ago

Question
What is 90%90\% of 4040? _____
Get tutor helpright-arrow

Posted 2 months ago

Question
What is the percent of change from 1212 to 2121?\newlineChoices: \newline(A) 75%75 \% increase \newline(B) 9%9\% decrease\newline(C) 75%75\% decrease\newline(D) 9%9\% increase
Get tutor helpright-arrow

Posted 2 months ago

Question
Is 1717 a prime number or a composite number? \newlineChoices: \newline(A) prime number \newline(B) composite number
Get tutor helpright-arrow

Posted 2 months ago

Question
2828 is what percent of 50? 50 ? \newline% \%
Get tutor helpright-arrow

Posted 4 months ago

Question
What is 2% 2 \% of 5050 ?
Get tutor helpright-arrow

Posted 4 months ago

Question
1212 is 60% 60 \% of what number?
Get tutor helpright-arrow

Posted 4 months ago

Question
2424 is 75% 75 \% of what number?
Get tutor helpright-arrow

Posted 4 months ago

Question
What is 84% 84 \% of 300300 ?
Get tutor helpright-arrow

Posted 3 months ago

Question
1515 is what percent of 25? 25 ? \newline% \%
Get tutor helpright-arrow

Posted 4 months ago

View all (153)