Full solution
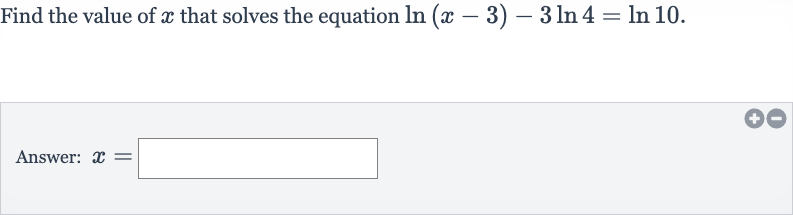
Q. Find the value of that solves the equation .Answer:
- Write Equation: Write down the given equation.We have the equation .
- Simplify Logarithms: Use the property of logarithms that to simplify the term with .
- Recognize Value: Recognize that is .
- Combine Logarithms: Use the property of logarithms that to combine the logarithms on the left side.
- Set Equal: If , then . So, set the inside of the logarithms equal to each other.
- Multiply by : Solve for by multiplying both sides of the equation by .
- Calculate Result: Calculate .
- Isolate x: Add to both sides to isolate .
- Add : Calculate .